728x90
반응형
3.11 부동소수점형
- 컴퓨터에서 실수(float)를 표현하거나 다룰 때 부동소수점형 사용
- 앞의 '부' 는 한자 뜰 부로, 소수점이 떠다니듯 움직인다는 뜻
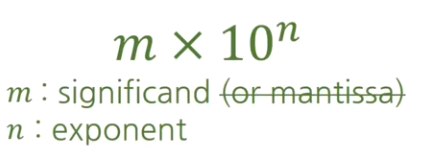
- 가수 부분을 뜻하는 mantissa라는 용어가 로그에서도 사용되는데 의미가 비슷하면서도 다르므로 가급적 사용하지 말자고 함 -> 대신 significand 사용

- 유효숫자(significant number)가 다르다 = 정밀도가 다르다 유효숫자가 많으면 많을수록 더 정밀해짐

- 실수를 컴퓨터에서 부동소수점 자료형으로 저장을 할 때 Normalized significand 형태로 바꿔서 저장
* 10진수(-314.625) -> 32bit 부동소수점 변환 예시
- 가수부는 mantissa 혹은 fraction

- 음수이므로 sign bit = 1
- -314.625 (10진수) = 100111010.101 (2진수) -> 1.00111010101 * 2^8
- 가수부에 소수점 아래 부분의 숫자들을 집어넣음
- 지수 8에 bias인 127을 더해줌 (bias는 2^k-1, k는 지수부의 bit수8) = 135
- 135를 2진수로 변환 = 10000111
- 변환한 2진수를 지수부에 집어넣음
- 결과 : 11000011100111010101000000000000

- 부동소수점을 사용하면 표현 범위가 훨씬 넓게 늘어남. 다만 메모리를 쪼개쓰므로 불리한 부분도 있음.
- 부동 소수점에선 정밀도를 보장하는 유효숫자가 6개
#include <stdio.h>
int main()
{
printf("%u\n", sizeof(float));
printf("%u\n", sizeof(double)); // float의 2배 크기
printf("%u\n", sizeof(long double));
float f = 123.456f;
double d = 123.456; // 리터럴 입장에선 기본형이 double
float f2 = 123.456;
double d2 = 123.456f; // 더 작은 size인 float을 더 큰 사이즈인 double에 넣으므로 정밀도 손해 X
int i = 3;
float f3 = 3.f; // 3.0f
double d3 = 3.; // 3.0
float f4 = 1.234e10f; // 1.234 * 10 ^ 10, 대문자 E도 사용 가능
float f5 = 0xb.ap1;
double d5 = 1.0625e0;
printf("%f %F %e %E\n", f, f, f, f); // %f %F는 차이 없음
printf("%f %F %e %E\n", d, d, d, d);
printf("%a %A\n", f5, f5); // %a = 16진수 출력
printf("%a %A\n", d5, d5);
return 0;
}
Output :
4
8
8 -> double과 동일한 크기. visual stuido에선 double과 long double의 크기가
8byte로 같으나 gcc 컴파일러에선 long double이 12byte
MS사에서 제공하는 컴파일러와 gcc에서 long double의 크기가 다름
123.456001 123.456001 1.234560e+02 1.829962E-304
123.456000 123.456000 1.234560e+02 1.829962E-304
0x1.7400000000000p+4 0X1.7400000000000P+4
0x1.1000000000000p+0 0X1.1000000000000P+0

3.12 부동소수점형의 한계
- Round off error : 컴퓨터가 유한한 자리수(비트들)로 수를 표현하면서, 반올림에 의해 수의 자리수를 줄일 때 발생
#include <stdio.h>
int main()
{
// round-off error ex1
float a, b;
a = 1.0E20f + 1.0f; // 앞 숫자가 너무 커 범위가 달라 상대적으로 작은 숫자인 1.0은 더해지지 않고 사라짐
b = a - 1.0E20f;
printf("%f\n", b);
// round-off error ex2
float c = 0.0f;
for (int i = 0; i < 100; i++)
c = c + 0.01f; // 2진수를 사용하는 부동소수점 표현법으로는 0.01을 표현할 수 없음
// 1/2, 1/4, 1/8... 등의 숫자의 조합으로 10진수를 만들어야 하는데 0.01처럼 깔끔하게 못 만드는 수가 많음
// 그 오차가 누적이 되어 1.0을 만들지 못함
printf("%f\n", c);
return 0;
}
Output :
0.000000
0.999999
#include <stdio.h>
#include <float.h> // 실수형의 표현 범위를 알려주는 library
int main()
{
// overflow
float max = 3.402823466e+38F; // float.h에 정의되에 있는 float이 가질 수 있는 가장 큰 숫자
printf("%f\n", max);
max = max * 100.0f;
printf("%f\n", max);
double maxd = 1.7976931348623158e+308; // double의 최대 숫자
printf("%f\n", maxd);
maxd = maxd * 100.0f;
printf("%f\n", maxd);
return 0;
}
Output :
340282346638528859811704183484516925440.000000
inf -> 너무 큰 숫자임을 표현
179769313486231570814527423731704356798070567525844996598917476803157260780028538760589558632766878171540458953514382464234321326889464182768467546703537516986049910576551282076245490090389328944075868508455133942304583236903222948165808559332123348274797826204144723168738177180919299881250404026184124858368.000000
inf
#include <stdio.h>
#include <float.h>
int main()
{
// underflow
float f = 1.401298464e-45F; // float이 가질 수 있는 가장 작은 숫자
printf("%e\n", f);
f = f / 2.0f;
printf("%e\n", f);
float f2 = 104.0f;
printf("%f\n", f2);
f2 = f2 / 0.0f;
printf("%f\n", f2);
return 0;
}
Output :
1.401298e-45
0.000000e+00 -> subnormal. 결과가 부동소수점형의 정밀도로는 표현할 수 없을 정도의 작은 숫자라서 사라져 버림
104.000000
inf
#include <stdio.h>
#include <math.h>
int main()
{
float f = asinf(1.0f);
printf("%f\n", f);
f = asinf(2.0f); // 수학적으로 asin2는 존재하지 않음
printf("%f\n", f);
return 0;
}
Output :
1.570796
-nan(ind) -> 수학적으로 존재하지 않는 표현 사용시 nan 출력 (nan = not a number)
강의 출처 : https://www.inflearn.com/course/following-c/dashboard
홍정모의 따라하며 배우는 C언어 - 인프런 | 강의
'따배씨++'의 성원에 힘입어 새롭게 개발된 C 언어로 시작하는 프로그래밍 입문 강의입니다. '따배씨'와 함께 프로그래밍 인생을 업그레이드 해보세요., 따라하며 배우는 C언어 '따배씨++'의 성원
www.inflearn.com
728x90
반응형
'Study_C, C++ > 홍정모의 따라하며 배우는 C언어' 카테고리의 다른 글
| [홍정모의 따라하며 배우는 C언어] 4.3 문자열이 메모리에 저장되는 구조 ~ 4.5 기호적 상수와 전처리기 (0) | 2021.08.16 |
|---|---|
| [홍정모의 따라하며 배우는 C언어] 3.13 불리언형 ~ 4.2 sizeof 연산자 (0) | 2021.08.13 |
| [홍정모의 따라하며 배우는 C언어] 3.9 고정 너비 정수 ~ 3.10 문자형 (0) | 2021.08.10 |
| [홍정모의 따라하며 배우는 C언어] 3.7 다양한 정수형들 ~ 3.8 8진수와 16진수 (2) | 2021.08.08 |
| [홍정모의 따라하며 배우는 C언어] 3.5 정수와 실수 ~ 3.6 정수의 오버플로우 (0) | 2021.08.07 |


