
- State Space Equation : System을 나타내는 다차의 미분 방정식을 다수의 1차 미분방정식으로 바꿔 Matrix로 표현한 방정식
- 확률론적 동적 System의 State Space 변화(한 Time Step에서 다음 Time Step으로의 State의 변화)를 나타낸다
- System의 State가 Input에 따라 어떻게 달라지는지를 나타냄
- System의 상태와 그 상태를 나타내는 수식의 집합
- State : 주어진 시간에서의 System의 상태를 나타내는 값 (Ex) 차량의 속도, 배터리의 온도 등)
- State Variable : System / Model의 상태를 나타내는 Variable
- State Space : 시간이 지나며 State Variable들이 변하는 공간. 초기 State로부터 접근 가능한 모든 State variable들을 모아놓은 것
- Kalman Filter와 같은 Estimator 사용 시 Modeling을 위해 사용한다
- State Space Equation은 위처럼 State Equation(상태방정식)과 Output Equation(출력방정식)의 2가지 식을 갖는다
- State Equation : 이전의 상태(Ex) 위치, 속도)와 현재 상태 간의 관계를 나타내는 방정식
- 현재 상태를 입력 및 과거 상태들로 구성한 방정식
- State Variable의 개수만큼 유도해야 함
- Output Equation : 현재 상태와 측정값 사이의 관계를 나타내는 방정식
- System의 출력을 입력과 상태변수들로 구성한 방정식이며 주로 다른 System 변수를 구하는데 사용
- A : State / System Matrix (n * n Square Matrix)
- 시간에 따른 상태의 변화를 야기하는 State Trasnsition Matrix (상태 천이 행렬)
- Input이 없을 때 시간에 따른 State의 변화를 나타냄
- B : Input / Control Matrix (n * m)
- Input에 따른 State의 변화를 나타냄
- C : Output / Transition Matrix (p * n)
- Output(y)과 State Variable(x) 사이의 관계를 나타내는 Matrix
- D : Forward Gain / Direct Transmission Matrix (p * m)
- Input이 Output Matrix에 미치는 영향을 나타낸 Matrix
- x : State Vector (n * 1)
- xdot : DIfferential of State Vector, System State`s change rate
- y : Output Vector (p * 1)
- u : Input Vector (m * 1)
- n : 상태 수, m : 입력 수, p : 출력 수
- State Equation은 아래와 같은 과정으로 구할 수 있다
- System Model 설정을 통한 계수 정리
- State Variable 설정
- State Variable을 미분한 것을 새로운 State Variable로 선언

Electrical Example)
http://www.senslab.co.kr/Class/%BB%F3%C5%C2%BA%AF%BC%F6%B8%F0%B5%A8.pdf
- 위 자료의 예제를 정리한 내용
- 아래의 관계식을 활용하여 위 Circuit의 Output인 Y를 구함
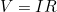



1. State Variable 설정

- Capacitor에 걸리는 전압과 Inductor에 흐르는 전류를 State Variable로 설정
- Elctrical System에서 State Space Equation을 사용할 경우, 위처럼 Capacitor 양단의 전압과 Inductor를 통과하는 전류를 상태 변수로 사용
- System의 에너지를 결정(저장)하는 값들
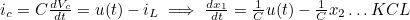

- 각 상태변수에 대한 계산식

- 회로에 저장된 Energy는 위와 같다
- 회로의 L, C 소자에 저장된 Energy
- 이에 따라 State Space Equation과 Measuremnt Equation을 작성하면 아래와 같다
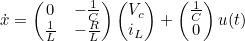

- State Variable의 시간에 따른 변화식 및 Input과의 관계식 계산을 통한 State Space Equation 구성
- State Variable과 Output의 관계식 계싼을 통한 Measurement Equation 구성
- Ex ) 아래와 같은 System의 State Space Equation 구하기

- System Model (위의 경우 운동 방정식) 설립
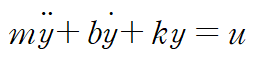
- 고계도함수의 계수가 1이 되도록 정리

- State Variable 설정 : x1 = y
- x1을 output에 해당하는 y로 정의

- x1의 미분을 두번째 State Variable로 정의
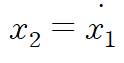
- 운동방정식에 y대신 x1을 대입

- x1'' 대신 x2', x1' 대신 x2 대입 (우변에 미분항이 없게 하기 위함)

- 이를 통해 얻은 두번째 State Equation과 그를 Matrix 형태로 변형


- State Variable x1을 선언할 때의 정의에 따라 Output Equation 정리

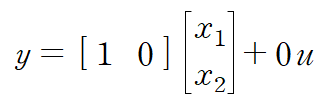
- Ex 2) System의 Model이 아래와 같다면

- 아래와 같이 Matrix로 State Variable을 표현할 수 있다
- x'', x', x 모두 System의 State를 나타내지만 System의 State를 나타내는데 이 3개의 Variable이 모두 필요하지는 않다
- 하나의 구속 조건인 방정식이 존재하므로 2개의 Variable의 값만 정해져도 System의 State를 알 수 있다

- 그리고 위의 미분 방정식을 아래와 같은 Matrix의 형태로 나타낼 수 있다

- 이 때 제어하고자 하는 변수가 x라 한다면

- Model의 미분 방정식과 관심 변수의 Matrix 식을 나열하면 아래와 같다

- 이를 State Space Equation이라 한다
- 그리고 다음과 같이 각 행렬식에 Laplace Transform을 적용하면 Transfer Function을 구할 수 있다

- 위는 입력이 하나인 단순한 경우이나 다수의 입력이 들어오는 경우 위와 같은 Matrix로 System을 표현하는 것이 계산에 용이하다
참고 자료 :
[자동 제어] 4. 상태공간표현법 및 전달함수
Transfer Function 2023.02.10 - [Automatic Control] - 2. Laplace Transform - 라플라스 변환 앞 글의 해를 가져오자. $$X(s) = \frac{\bar{U}(s)}{s^2+2\zeta\omega s + \omega^2}$$ 이는 이렇게 표현할 수 있다. $$\frac{X(s)}{\bar{U}(s)} = \
dongmin-archive.tistory.com
https://subprofessor.tistory.com/128
[동역학] 상태공간 모델(State-space model), 전달함수(Transfer Function)
#동역학 #시스템해석 https://search.shopping.naver.com/book/catalog/32464065666 System Dynamics : 네이버 도서 네이버 도서 상세정보를 제공합니다. search.shopping.naver.com 1. State Equation & Output Equation (1) State Equation
subprofessor.tistory.com
https://lpsa.swarthmore.edu/Representations/SS/SS2SSDetails.html
Details of Case 2: State Space to State Space
We now restate the original state representation and plug this definition of q, and solve
lpsa.swarthmore.edu
http://www.senslab.co.kr/Class/%BB%F3%C5%C2%BA%AF%BC%F6%B8%F0%B5%A8.pdf
'Study_Engineering' 카테고리의 다른 글
| 표준편차, 분산, 공분산 (0) | 2024.01.16 |
|---|---|
| EKF를 통한 자율주행 로봇의 Localization (3) | 2024.01.15 |
| About Electric Circuit (1) | 2024.01.08 |
| About Avg, MovAvg, LPF (0) | 2023.12.22 |
| 전기/전자 관련 기초 지식 (0) | 2023.12.15 |



