728x90
반응형
1. 표준 편차 (Standard Deviation)
- Mean(평균)에 대한 오차 범위를 나타냄
- 클수록 Data들이 퍼져있는 정도가 큼을 의미
- 단 아래처럼 데이터에 양수와 음수가 섞여있는 경우, 서로의 차이값이 상쇄되어 알고자 하는 값이 나오질 않음
| A | B | C | D |
| 5 | 10 | -10 | -15 |
- 평균 : 5 + 10 - 10 - 15 = -10
- 표준 편차 : (5-10) + (10-10) + (-10-10) + (-10 -15) = -60
- 따라서 이 편차들을 제곱하여 합하는 Variance (분산)에 루트를 씌운 값을 표준 편차로 사용함

2. Variance (분산)
- 각 Data들의 편차의 제곱의 합
- 확률변수의 경우 확률변수 하나의 분포 상태를 나타내는 값
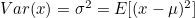
- Variance 계산식
- Variable이 Discrete(이산) / Continous(연속)이냐에 따라 아래와 같은 계산식을 가짐

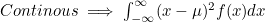
3. Covariance (공분산)
- 2개의 확률변수 간의 선형 관계를 나타내는 값. 추정값의 정확도를 보이는 역할
- 계산 결과값이 양수일 경우 서로 비례, 음수일 경우 서로 반비례 관계임을 의미
- 서로 독립관계이면 0 (역은 성립 X -> 서로 독립이 아니여도 0이 나올 수 있음)
- 추정 오차는 이 Covariance에 비례

- Covariance(공분산)는 두 확률변수 간의 선형관계를 나타냄


- Covariance 계산식
- E는 괄호 내 변수의 평균을 구하는 연산자
- 마찬가지로 Discrete / Continous에 따라 아래와 같은 계산식을 가짐


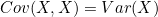
- 서로 같은 변수에 대한 공분산은 분산과 같다
728x90
반응형
'Study_Engineering' 카테고리의 다른 글
| Extended Kalman Filter란 (0) | 2024.01.16 |
|---|---|
| Kalman Filter란 (0) | 2024.01.16 |
| EKF를 통한 자율주행 로봇의 Localization (3) | 2024.01.15 |
| State Space Equation이란 (0) | 2024.01.12 |
| About Electric Circuit (1) | 2024.01.08 |



