0. 목적
- Extended Kalman Filter를 통해 주어진 환경에서 자율주행 Robot의 Localization (위치 파악) 진행
1. 전체 과정
- Odometry 계산
- State Vector 정의 -> State Space Model / Measurement Model 정의
- Linearization을 위해 State Space Model / Measurement Model에 대한 Jacobian Matrix 계산
- System / Sensor Noise Model (Covariance Matrix) 정의
- 위 Model들에 대해 EKF의 Prediction - Update 과정을 재귀적으로 진행
* 본 예제는 ROS 기반의 Navigation Stack이 구성되었다는 가정 하에 진행
관련 내용 : https://youngseong.tistory.com/130
[RIS] 1/11 (Navigation Stack 구성 완료)
- 아래의 내용들을 토대로 Robot의 전체적인 Software 구성 https://youngseong.tistory.com/102 [KUSMO] 11/4 (Navigation Stack 구성법) 로봇의 ROS Navigaion Stack 구성 Navigation stack은 로봇을 시작점에서부터 목적지까지
youngseong.tistory.com
https://automaticaddison.com/extended-kalman-filter-ekf-with-python-code-example/
Extended Kalman Filter (EKF) With Python Code Example – Automatic Addison
In this tutorial, we will cover everything you need to know about Extended Kalman Filters (EKF). At the end, I have included a detailed example using Python code to show you how to implement EKFs from scratch. I recommend going slowly through this tutorial
automaticaddison.com
- 위 게시물을 참고하여 작성한 글
2. 상세 과정
2.1 각 바퀴의 Encoder 값을 통해 Odometry 계산
- 각 바퀴의 Encoder값을 통해 이동거리를 계산하여 Odometry 계산
- Odometry : 시작 지점으로부터의 상대적인 위치
- 바퀴의 Encoder Data를 통해 주어진 공간 상의 Robot의 위치와 방향을 시간이 지남에 따라 estimate한다
- 즉, 각 시간간격에 따른 Wheel Encoder Data에 Trigonometry(삼각법)를 계산하여 Robot의 위치를 estimate한다
- 본 예제는 Extended Kalman Filter를 중점적으로 설명하는 것이 목적이므로 자세한 계산 과정은 생략
- 관련 내용 : https://automaticaddison.com/how-to-describe-the-rotation-of-a-robot-in-2d/
How to Describe the Rotation of a Robot in 2D – Automatic Addison
In this post, we’ll take a look at how to describe the rotation of a robot in a two-dimensional (2D) space. Consider the robot below. It’s moving around in a 2D coordinate frame. Its position in this coordinate frame can be described at any time by its
automaticaddison.com
2.2. State Space Equation정의
- State Space Equation은 Dynamic System의 한 Time Step에서 다음 Time Step으로의 State 변화를 나타낸다
- 본 예제의 경우, State Space Equation의 활용은 아래와 같이 이뤄진다
State Space Equation을 통해 Robot의 Position과 Orientation이
Control Input (본 예제의 경우 Velocity Command)에 따라 어떻게 영향을 받는지 나타냄
- 즉, 한 Timestep에서부터 다음 Timestep까지의(k-1 -> k) Robot의 Motion을 나타냄
- 이를 위해선 우선 Robot의 State Variable부터 정해야 한다
2.2.1 State Variable 정의
- State Variable 이란 현재 System의 State를 표현하는 Variable들을 의미한다
- 여러 값들을 임의로 정할 수 있다
- 본 예제에서는 Robot의 State Variable을 아래와 같이 정하였다

- Xk, Yk : Robot의 X, Y 좌표
- γk : Robot의 Yaw Angle(Z축 기준의 회전 Angle)

- X, Y, Z 축 각각에서의 회전은 Roll, Pitch, Yaw라 칭한다
- 위 모습을 Z축 위에서 바라보면 아래와 같다

- Trigonometry에 의해 Robot의 Velocity V는 아래와 같이 계산할 수 있다

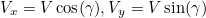
- 위의 Vx, Vy가 Robot의 X, Y 축에 대한 Linear Velocity에 해당된다

- Z축에 대한 Angular Velocity는 위와 같다
- 거리 = 속도 x 시간임을 이용하면 아래와 같이 Robot의 Motion을 수학적으로 표현할 수 있다

- 위 식은 sin, cos 식이 포함된 Non Linear Equation이다
- 이를 아래와 같이 Linearization 후 Extended Kalman Filter에 적용시켜야 한다


- 위가 변환하고자 하는 Linear State Space Equation의 형태이다
- 각 변수의 의미는 아래와 같다
- Xk : 현재 Timestep에서의 전체 State Variables
- Xk-1 : 이전 Timestep에서의 전체 State Variables
- Ak-1 : System의 State가 Control Command 없이 시간 k-1 -> k 에서 어떻게 변하는지를 나타내는 Matrix
- Bk-1 : System의 State가 Control Command에 의해 시간 k-1 -> k 에서 어떻게 변하는지를 나타내는 Matrix
- Uk-1 : Control Input. 본 예제의 경우 Control Input은 아래와 같은 Linear / Angular Velocity임
- 이 Linearization 과정은 Jacobian Matrix 계산을 통해 수행할 수 있다
- Jacobian Matrix : 다변수 벡터 함수의 도함수 Matrix
- 편미분 행렬으로, 미소 영역에서의 Linearization에 사용
2.2.2 A Matrix (System Matrix) 정의
- System Matrix는 Control Input이 없을 때, 시간이 지남에 따라 (k-1 -> k) 변하는 System의 State를 나타냄
- 즉, 시간에 따른 State의 변화를 야기하는 State Transition Matrix (상태 천이 행렬)
- A Matrix의 행과 열 각각은 State의 수와 동일
- 앞서 구한 Non Linear 형태의 Motion Equation을 Jacobian Matrix 계산을 통해 Linearization 시켜야 함
- A Matrix의 Jacobian Matrix 계산 식은 아래와 같다

- 위의 수많은 편미분 중 1열 1행 만을 계산해보면

- 위와 같은 과정으로 9개의 편미분을 각각 풀면 아래와 같은 결과가 나온다

- Robot의 바퀴는 Velocity Command에 의해서만 움직이므로 위와 같이 Identity Matrix 형태의 결과가 나옴
- 즉 Velocity Command 외에는 State의 변화를 일으키는 요소가 없음
- Velocity Command가 없을 때 System의 State에 영향을 주는 요인이 있으면 A Matrix는 다른 형태를 띄게 됨
2.2.3 B Matrix (Input Matrix) 정의
- Input Matrix는 Control Input에 의해 System의 State가 k-1에서 k 변하는 System의 State를 나타냄
- 즉 Input에 따른 State의 변화를 나타냄
- B Matrix의 행의 수는 State의 수, 열의 수는 Control Input ( [v, w] )과 같다
- A Matrix와 마찬가지로 B Matrix에 대한 Jacobian Matrix를 계산하면 아래와 같다

2.2.4 State Space Equation 정의
- 이에 따라 구하고자 했던 State Space Equation의 전체 형태는 아래와 같다

- 그리고 Robot이 항상 명령한대로 움직이진 않으므로 이에 대한 Noise(System Noise)를 더한 최종 식은 아래와 같다

- 이 식을 통해 아래와 같은 사실을 알 수 있다
Robot의 현재 위치(x, y), 회전각(γ), Linear Velocity(Vx, Vy), Angular Velocity(ω), 시간 간격(Δt)을 알면 다음 Timestep에서의 Robot의 State를 알 수 있다
2.3. Measurement(Observation) Equation 정의
- Measurement Equation은 Noise가 포함되어 있는 측정 Sensor 값과 예측 Sensor 값을 비교하여
시간 k에서의 System의 State에 대한 최적의 추정값을 도출한다 - Robot이 공간을 주행할 때, Robot의 State를 추정하기 위해 Sensor를 통해 측정값을 얻음
Measurement Model은 이와 반대로 현재 Timestep에서의 예측 State값을 통해 Sensor 값을 예측
- Sensor 값에 Noise가 많아 신뢰하기 어렵거나 Sensor 자체의 문제로 이상한 값을 내는 경우
Measurement Model을 통해 현재 Timestep에서의 Sensor값을 예측할 수 있다
- Robot을 시작점에서부터 목표지점까지 이동시키고자 할 경우 Robot의 위치와 이동방향(State Variable)을 알아야 함
- 예측 Sensor 값과 실제 Sensor 값의 Weighted Average를 계산하여 상태에 대한 최적의 추정값 도출 가능
- 위는 Kalman Filter의 Kalman Gain 계산 과정에 해당한다

- Measurement Model은 위처럼 Time k에서의 예측 Sensor 값의 벡터 y를 Time k에서의 System의 State에 대한 함수 형태로 나타내고 그에 Sensor Noise를 결합한 수식
- Yk : 시간 k에서의 n개의 예측 Sensor 값
- wk : n개의 Sensor값 각각에 대한 Noise
즉 k-1의 State 값으로부터 k에서의 State를 예측한 후에
그 예측 State 값을 통해 그에 상응하는 Sensor값을 예측
2.3.1. H Matrix (Output Matrix) 정의
- Output Matrix는 Output과 State Variable 사이의 관계를 나타냄
- 이를 통해 시간 k에서의 예측 State 추정치를 k에서의 예측 Sensor 값으로 변환시킴

- 행은 Sensor 측정값의 개수, 열은 State 수와 동일
- Sensor 값으로 State 값을 바로 알 수 있다면 H Matrix는 아래와 같은 Identity Matrix가 됨

- Ex) 2D 상에서의 상대 위치 및 각도 추정
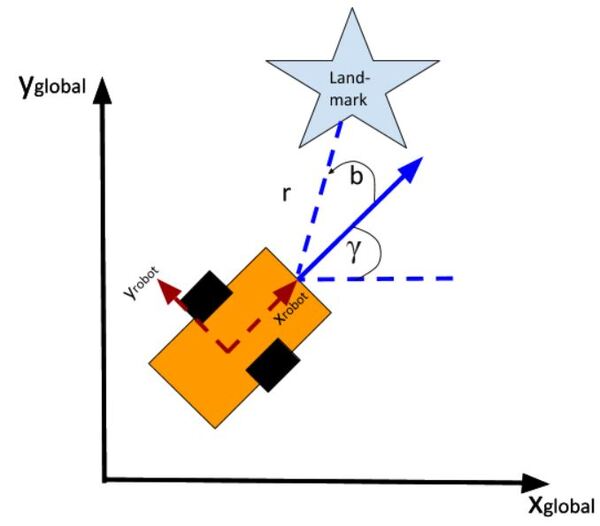
- 위처럼 LandMark가 있을 경우, Robot과 LandMark 간의 거리 r과 Bearing Angle b를 계산하는 방법

- Trigonometry와 Pythagorean Theorem에 의해 두 값을 계산할 수 있다
- 위 식을 Matrix 형태로 나타내면 아래와 같다

- 위 식은 arctan으로 인해 Non Linear 특성을 띈다
- 따라서 State Space Equation에서와 마찬가지로 Jacobian Matrix 계산을 통한 Linearization을 진행하여야 한다

- 따라서 위 예제에 대한 Measurement Model의 전체적인 형태는 아래와 같다


- 위 식은 아래와 같이 나타낼 수 있다
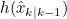
2.4. Extended Kalman Filter

- 앞서 언급했던 Robot의 State Vector
- Sensor를 통해 이 State들을 계산할 수 있으나, Noise가 섞여있고 시간 간격(Δt)간에 크게 변할 수 있어
Sensor 값 만으로는 Robot의 위치 계산을 정확히 할 수 없다- Robot이 이동함에 따라 계산되는 State Vector는 '추정치'

- 앞서 구한 Robot의 State Space Equation
- 위를 통해 현재 Timestep 에서의 Robot의 상태를 알 수 있다

- 그리고 위의 Measurement Equation을 통해 현재 Timestep에서의 State 추정값으로
k에서의 Sensor 측정값 벡터를 추정할 수 있다- Sensor를 통해 State Variable을 직접 측정할 수 있다 가정
- Noise는 임의의 값 설정 (±0.07m, ±0.04rad)
- 이후로의 Extended Kalman Filter 적용 과정은 아래와 같다
- Prediction Step
- k-1에서의 State 추정치와 Input(Velocity Command)을 통해 k에서의 State 예측
- k-1에서의 Covariance와 Noise를 통해 State Covariance 예측
- Update Step
- Kalman Gain 계산
- 예측 State 값을 통해 Sensor 측정 값 예측
- k에서의 실제 Sensor 값과 예측 Sensor 값의 차이 계산
- 위의 차이와 Kalman Gain을 통해 예측 State값을 Update
- k에서의 Updated 오차 Covariance 계산
* Covariance : 두 변수가 서로 얼마나 다른지를 계산. 결과값이 양수일 경우 서로 비례, 음수일 경우 반비례 관계임을 의미
0일 경우 둘은 서로 독립적 관계
3. Extended Kalman Filter 상세 과정
3.1. Initialization
- 시작 시점은 k
- k-1에서의 State / Control Vector 초기화

- Robot의 초기 위치는 아래와 같다
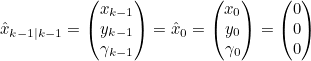
- 그리고 k-1에서의 Control Input은 없었다고 가정한다
- Vk : Linear Velocity
- Wk : Angular Velocity (Yaw)

3.2 Predict State Estimation

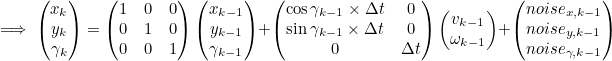
- 위 식을 통해 Robot의 k에서의 State 예측
3.3 Predict Covariance of State Estimation
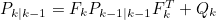
- P_k-1|k-1은 State의 수와 같은 수의 행과 열을 갖는 Square Matrix
- 전 과정에서의 State 예측값의 정확도를 나타내는 행렬
- 대각 성분이 Variance (분산), 나머지 부분이 Covariance(공분산)
- Variance : 확률 변수 하나의 분포 상태를 나타냄
- Covariance : 두 확률 변수 사이의 선형 관계를 나타냄
- 초기에는 아래처럼 임의의 추정값 대입
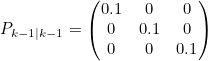
- Fk는 State Space Equation에서 구한 Ak(System Matrix)와 동일
- Control Input이 없을 때의 k-1 -> k 에서의 System State의 변화를 나타냄
- Robot은 속도 명령에 의해서만 움직이므로 본 예제에선 Identity Matrix의 형태를 띔

- Qk는 System Model Noise로, 마찬가지로 Square Matrix임
- State 수와 행, 열이 동일한 Square Matrix
- Robot의 실제 Motion과 추정 State Space Model 간의 편차를 나타냄
- Robot은 항상 명령한대로 움직이진 않는다
- 따라서 예측 State 추정 값 그대로 실제 State가 나오진 않음
- Q가 클수록 Sensor 측정값의 변화를 더 자세히 추적함
- 예측 Sensor 값보다 실제 Sensor 측정값을 더 신뢰한다는 뜻

- 동일한 두 변수의 Covariance는 Variance임
- 아래와 같이 Identity Matrix로 시작해서 시행착오에 따라 값을 바꿀 수 있음

- 이에 따라 State Estimation 값의 예측 Covariance는 다음과 같다


3.4. Calculate Kalman Gain

- Kalman Gain은 새 Sensor 측정값을 통해 예측 State값과 그 값의 Covariance가 얼만큼 보정되어야 하는지를 나타냄
- Sensor Noise가 크면 Kalman Gain값을 낮춰 Sensor 측정값을 State 추정에 거의 반영하지 않도록 해야 함
- Dynamic Model을 통한 예측값의 Noise가 크면 K의 크기를 키워(1에 근사하게) Sensor 측정값이 State 추정에 큰 영향을 미치도록 함
- 위 식의 괄호 안의 값을 따로 분리하여 Sk로 표현할 수 있다
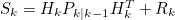
- 위 Matrix는 예측 Sensor 값의 Covariance를 나타낸다
- Rk는 Sensor의 Noise Covariance Matrix로, Sensor 측정값의 갯수와 같은 수의 행, 열을 갖는다
- Qk와 마찬가지로 초기에는 Identity Matrix로 시작해서 시행착오에 따라 값을 바꿀 수 있음

3.5 Update State Estimate
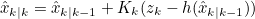
- 앞서 계산한 예측 State 추정값과 Kalman Gain, 실제 Sensor값과 예측 Sensor값의 비교를 통해 State 추정값 Update
- 즉 새 Sensor 값 측정 이후 Robot의 State를 나타냄
이 Update된 State 값이 Extended Kalman Filter를 통해 구하고자 했던 Robot의 State

- 실제 Sensor 값과 예측 Sensor 값 비교
- Zk : Measurement Vector
- 본 예제에서는 State Variable 3개를 Sensor로 직접 측정할 수 있다 가정하였으므로
Measurement Vector는 아래와 같다
- 본 예제에서는 State Variable 3개를 Sensor로 직접 측정할 수 있다 가정하였으므로

- h( ... ) : Measurement Model
- Measurement Model은 아래와 같다

- Hk : Measurement Matrix
- 본 예제의 경우 Sensor 값으로 State 값을 직접 측정할 수 있으므로 Identity Martix가 된다

- Wk : Sensor Noise
- 본 예제에서는 앞서 아래의 임의의 값으로 설정했음
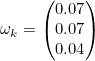
3.6 Update Covariance of State Estimate
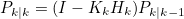
- 예측 Covariance, Update된 State 추정값의 Covariance Update
- 즉 새 Sensor 값 측정 이후 Robot의 Covariance를 나타냄
4. 결론
Wheel Encoder 값을 통해 계산한 Odometry Data로 Robot의 State를 예측하고
이를 IMU Data를 통해 보정하여 주어진 환경에서의 Robot의 위치를 추정
- 예측 State 값과 Sensor 값을 섞어 더 나은 State 값을 추정함
'Study_Engineering' 카테고리의 다른 글
| Kalman Filter란 (0) | 2024.01.16 |
|---|---|
| 표준편차, 분산, 공분산 (0) | 2024.01.16 |
| State Space Equation이란 (0) | 2024.01.12 |
| About Electric Circuit (1) | 2024.01.08 |
| About Avg, MovAvg, LPF (0) | 2023.12.22 |



