728x90
반응형
0. About Battery Modeling
- Analog Electric Circuit을 통해 전류가 입력됐을 때의 Battery의 전압 응답을 Equivalent Circuit Model을 통해 근사
- 이를 통해 Battery의 동작을 간단하게 모사하는 방식에 대한 내용
1. Equivalent Circuit Model
- 아래의 Thevenin Equivalent Circuit을 통해 Battery의 입력 전류에 대한 전기화학적 반응 모사
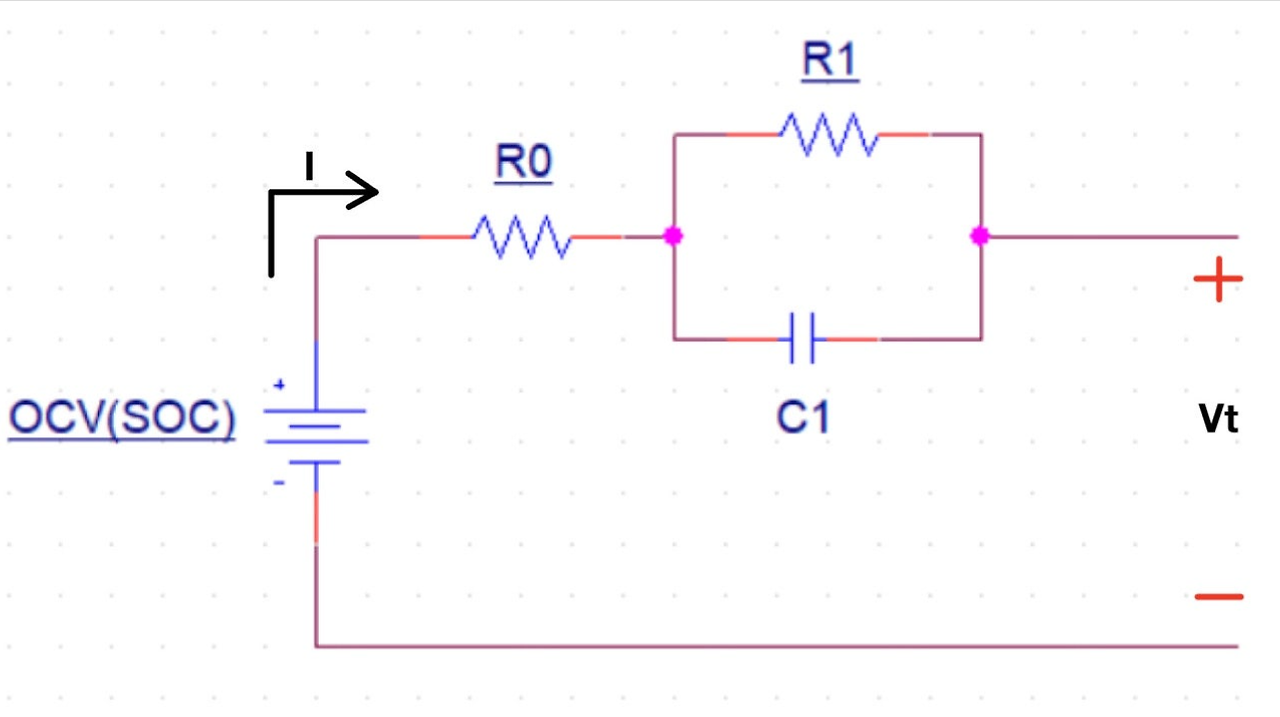
- 위 등가회로의 방정식이 Battey의 동작을 근접하게 묘사함
- 이러한 Model을 Equivalent Circuit Model이라 부름
- Battery의 구조를 묘사하는 것이 아닌 Battery의 일부를 표현
- 이 ECM은 구현이 단순하고 안정적으로 동작하여 최근 BMS에서 Battery의 적절 동작 범위 유지에 활용함
- ECM을 통한 예측 동작과 Battery의 실제 동작 간의 차이를 Modeling Error라 함
- 이 Error를 분석하고 Model을 다듬어 이를 최소화하는 것이 목적
1.1. ECM 구성 과정
1) Constant Voltage Source : Open Circuit Voltage

- Cell이 단자에서 전압을 운반하는 것을 단순한 이상적 전압원으로 표현
- Vt는 it, Cell의 사용 이력에 무관한 정전압(Constant Voltage)
- 실제로는 위의 요소를 포함한 다른 요인에도 영향을 받음
- 위 상태는 Voltage Source에 Load가 연결되지 않은 Open Circuit 상태로, Vt는 Equilibrium 상태가 된다
- 따라서 Unload 상태에서 측정한 Voltage 값인 OCV를 Voltage Source로 사용한다
- OCV (Open Circuit Voltage) : 부하가 걸리지 않은 상태에서의 전압값
2) OCV - SoC 관계 반영
- OCV와 SoC의 관계를 활용
- OCV는 SoC에 따라 달라지며 완충 상태의 OCV가 방전됐을 때의 OCV보다 높음
- SoC (State of Charge) : 충전량. 완충 시 100(%), 완방 시0(%)
이러한 OCV와 SoC의 상관 관계를 ECM에 반영

- 위의 OCV - SoC Lookup Table은 실험을 통해 구해야 함
- 위 실험 후 SoC 100 -> 0으로의 방전 시 제거된 전하의 양을 나타내는 지표인 Total Capacity, Q [Ah]를 정의
- 온도나 전류에는 무관하나 기생성 화학부반응과 전극 구조의 손상으로 인한 열화에 따라 점진적으로 감소
- 이를 아래의 상미분방정식으로 표현 가능
- 상미분방정식(Ordinary Differential Equation) : 구하려는 함수가 하나의 독립 변수만을 갖고 있는 미분 방정식

- SoC 위의 점은 아래의 시간에 대한 미분을 의미하며 시간에 따른 전류 함수 i(t)는 방전이 양수

- 위 식에서 i(t)의 단위가 Ampere이므로, 계산을 위해선 Q를 Ampere - Seconds로 변환해줘야 함
- η : Cell의 Coulombic Efficiency(쿨롱 효율. 충전 용량 대비 방전 용량의 비율)을 의미
- 아래처럼 전류에 따른 값을 갖는다

- 충전 시, Cell을 통과하는 일부 Charge들이 의도치 않은 부반응에 참여하여 Cell의 SoC를 증가시키지 못하는 경우가 생긴다
- 이로 인해 Cell의 Coulombic Efficiency가 감소할 수 있다
- 단 리튬 이온은 높은 안정적 구조로 인해 보통 Coulomb Effeciency를 1로 가정함

- 시간에 따른 SoC의 변화에 관한 식
- 𝛕 : 시간 변수에 대한 Placeholder

- 위의 연속 시간 방정식을 BMS의 MCU에 적용하기 위해 이산 시간 방정식으로 변환

- 정전압원이 SoC에 따라 변하는 종속전압원 OCV(SoC(t))로 대체됨
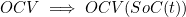
- 여기서 온도에 대한 상관관계를 추가하면, 전압원은 아래와 같이 변경됨
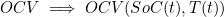
- T(t) : 시간 t에서의 Cell의 내부 온도
3) 직렬 저항 추가
- 시간에 따라 변하는 전류가 인가되었을 때의 Cell의 반응을 모사할 동적 특성 추가
- 우선 부하 연결 시의 전압 강하와 충전 시의 상승 현상을 모사
- 방전 시 OCV아래로, 충전 시 OCV 위로 전압이 변하는 현상
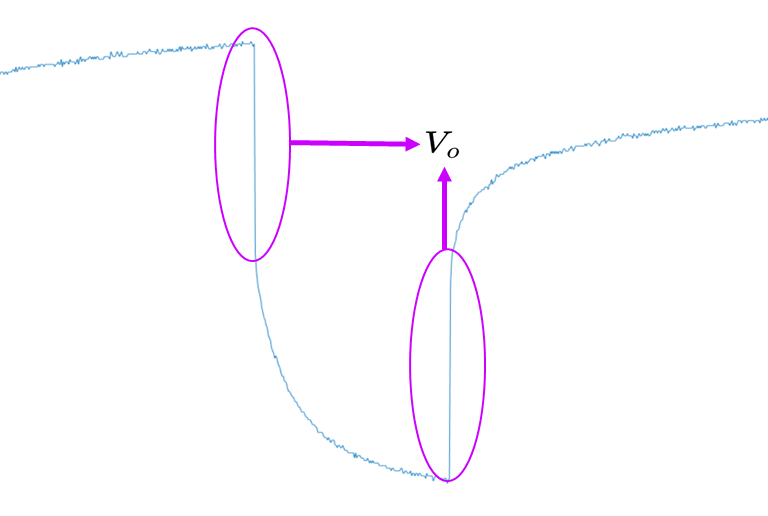
- 위처럼 전류 인가 및 제거 직후 Cell의 순간적인 반응을 아래와 같이 OCV와 직렬로 연결된 저항 하나로 표현 가능
- 이 R0는 Cell의 내부 저항을 표현하는 역할
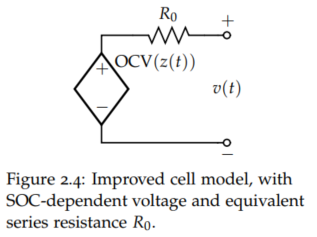
- R0에 걸리는 전압 V0가 위의 순간적인 전압 강하의 정도를 표현
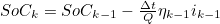
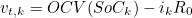
- 기존의 SoC 식에 단자 전압 V(t)의 계산식 추가
- R0가 추가됨으로 인해 Power 일부가 열로 소모되고, 이로 인해 Cell의 에너지 효율이 완벽해지지 않음
- R0로 인한 Power 소모량은 아래와 같다
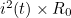
- Cell의 내부 저항도 SoC와 온도에 따라 달라지므로, 이를 R0에 반영하여 ECM의 정확도를 높일 수 있다
4) Diffusion Voltage 추가
- 순간적인 전압 강하 직후의 Cell의 동적 전압 반응 모사
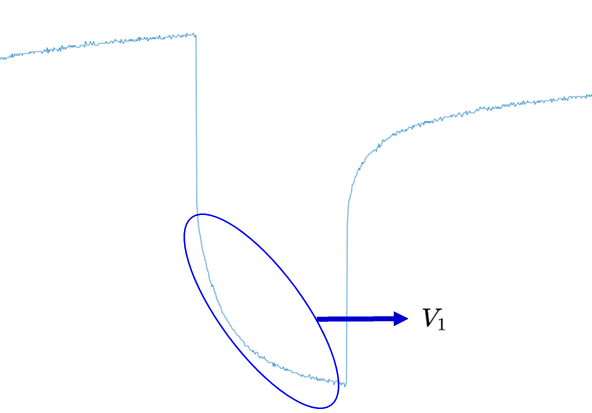
- 위 부분을 ECM으로 모사
- 위 현상은 리튬의 느린 확산 현상때문에 일어남
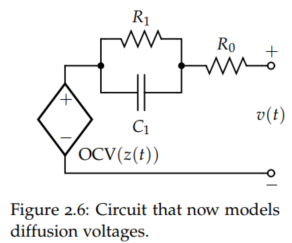
- RC 병렬 구조에 걸리는 전압 V1이 동적 반응을 표현
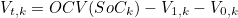
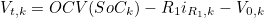
- V(t) 계산식에 RC 병렬 구조에 대한 항이 추가됨
- iR1_k 계산식 유도 과정 : KCL 활용
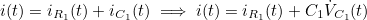
- 직렬 저항과 RC Ladder가 만나는 Node에 대한 KCL 계산
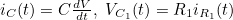
- 위의 Capacitor 전압식을 KCL 수식에 대입하면
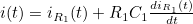
- 위와 같은 수식이 나오고, 이를 R1의 미분식에 대해 정리하면
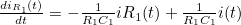
- 위와 같은 수식이 나오고, 이를 상태공간방정식의 형태로 정리하면
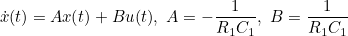
- 위와 같이 정리된다
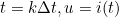
- 이 연속방정식을 이산시간으로 변환하기 위해 위 값을 적용하여 아래의 상태방정식 형태로 변형 후 적분
- 입력은 일정한 정전류라 가정
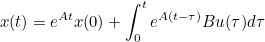
- 위 수식은 초기 상태 x(0)와 입력 u(t)의 비율을 나타냄
- 적분 계산식은 Convolution
- Convolution : 한 f함수와 다른 함수를 반전 이동한 함수 g를 곱한 후 적분하여 새로운 함수를 구하는 수학 연산자
- 신호를 Filtering / Sampling 하거나 Laplace Transform, Fourier Transform에서 사용
- f는 본래 신호
- g는 Filter, 가중치
- 함수 f가 주어졌을 때 목적에 따라 함수 g를 선정하여 분해, 변환, 필터링 할 수 있다
- 수식 유도 과정
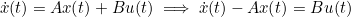
- Ax(t) 항을 좌항으로 넘긴 후 위 식 양변에 exp(-At)를 곱함
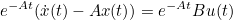
- 이 때, 좌항은 아래처럼 exp(-At)x(t)를 미분한 형태이다
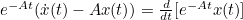
- 위를 좌항에 대입
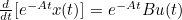
- 이후 양변을 시간 0 -> t에 대해 적분하면
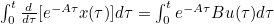
- 이고, 위 식의 좌변을 계산하면
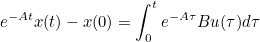
- 이고, x(0)을 우항으로 넘기고 양변에 exp(At)를 곱하면
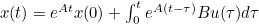
- 이후 위 식에 이산 시간 변환 식 적용
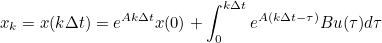
- 위 식의 우항을 [0, (k-1)Δt]와 [(k-1)Δt, kΔt]로 분리
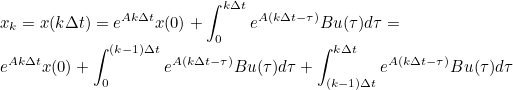
- 위 식의 우항에서 [0, (k-1)Δt] 적분 구간 항에서 exp(AΔt)를 따로 분리 후 묶음
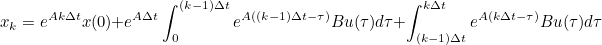
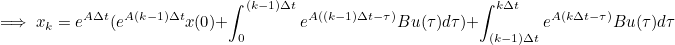
- 위 식에서 exp(AΔt)로 묶인 부분은 아래의 전 Step에서의 State와 같다
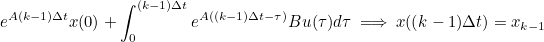
- 위 내용을 수식에 적용하면
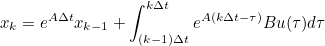
- 이고, 위 식의 우항의 적분식에서 exp(AkΔt)를 앞으로 빼면
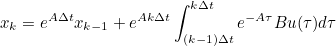
- 가 되고, 우항의 Bu(𝛕)가 (k-1)Δt -> kΔt 동안 u((k-1)Δt)로 일정하다 가정하면 아래처럼 Bu_k-1 항을 빼낼 수 있다
- 방전 전류가 해당 Time Step 동안 일정함을 의미
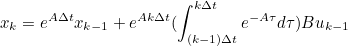
- 이후 우항의 적분식을 계산하면
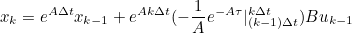
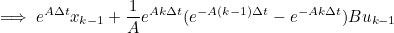
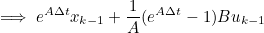
- 위 과정을 통해 구한 수식은 아래와 같다
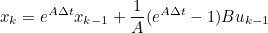
- 위 식은 이산시간에서의 상태방정식과 동일한 형태이다
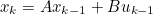
- 위 식에 앞서 구한 아래의 상수값들을 대입하면
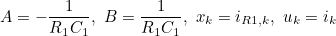
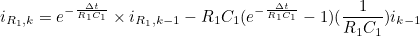
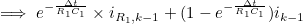
- 위와 같은 식을 얻을 수 있다
위 식이 저항 R1에 흐르는 전류에 대한 이산 시간 방정식

- 지금까지의 내용을 정리하면, 위의 ECM을 나타내는 방정식은 아래와 같다
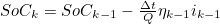
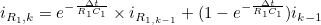
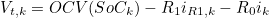
- 첫번째 식은 전류적산법 식이다
- 두번째의 i_R1,k 식을 세번째의 ECM의 출력 전압 계산 식에 대입하면 아래와 같은 식을 얻을 수 있다
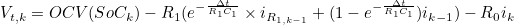
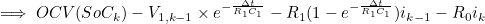
위 식이 ECM의 측정방정식에 해당한다
1.2. ECM 계산 예시 (위의 R0, R1-C1 연결 구조)
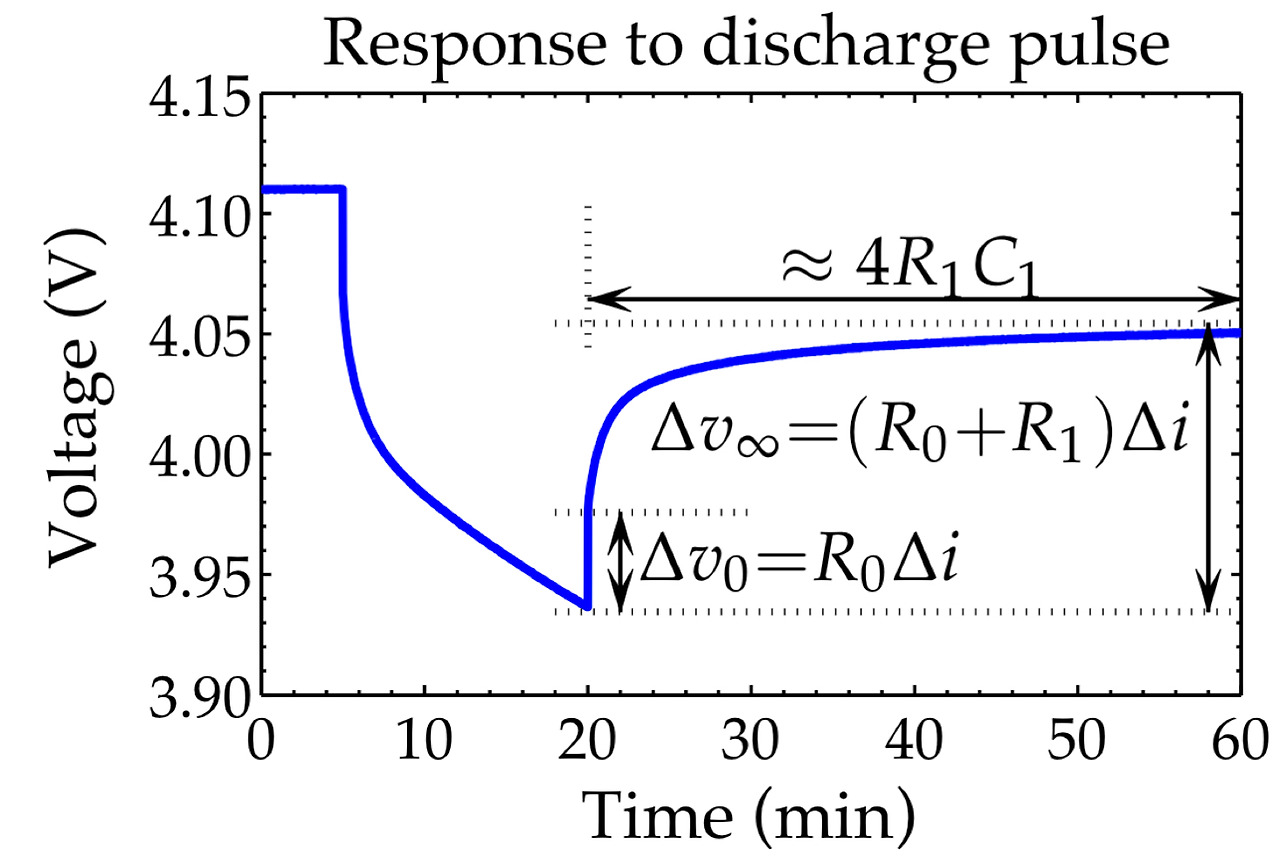
- 입력 전류 인가 직후, 제거 직후의 즉각적인 전압 응답은 아래와 같다
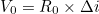
- Capacitor의 전압은 순간적으로 변할 수 없고, SOC는 전류가 0일 때는 바뀌지 않기 때문
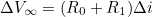
- 이후 Steady State에서 Capacitor의 전압은 0으로 수렴한다
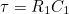
- 시정수 𝛕는 위와 같다
- 위처럼 방전류에 대한 Cell의 전압 응답을 계산하여 ECM의 Parameter들을 계산할 수 있다
2. Hysteresis Voltage
- 이론적으로는 Cell의 전류가 0이 되면 V0가 바로 0으로 떨어지고, VC1도 R1에 의해 방전되어 0으로 감소하고, 이로 인해 Cell의 단자 전압이 OCV에 수렴하게 된다
- 하지만 실제로는 OCV와는 다른 값으로 수렴하게 된다
- 이는 Cell의 최근 사용 이력에 따라 달라진다
- Ex) SoC 50%로 방전 후 휴지기간 부여 시 OCV보다 낮은 전압값으로 수렴
- SoC 50%로 충전 후 휴지기간 부여 시 OCV보다 높은 전압값으로 수렴
- 이는 Cell의 단자전압이 Hysteresis가 존재함을 나타낸다
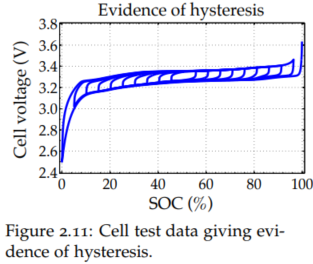
- Cell 완충 후 SoC 0%까지 1/30 C Rate로 방전 (아래쪽 곡선)
- 이후 1/30 C Rate로 SoC 95%까지 충전 후 5%까지의 방전을 반복
- 위쪽과 아래쪽 곡선 간의 공간으로 인해 모든 SoC마다 가능한 휴지 값의 범위가 있음을 발견함
- LFP Cell의 경우 SoC 간의 전압값 차이가 크지 않아 이 Hysteresis Voltage를 잘 Modeling하여 예측한 휴지 단자 전압과 OCV가 얼마나 차이가 나는지를 알아야 한다
- Hysteresis와 Diffusion Voltage는 서로 구분하여야 한다
- Diffusion Voltage의 경우 시간에 따라 달라지나 Hysterersis Voltage는 SoC가 변할때만 변한다
- Diffusion Voltage는 휴지 기간에서 사라지나 Hysteresis Voltage는 전혀 변하지 않는다
- Hysteresis Model은 이를 잘 파악하여야 한다
- 단순한 Model은 전류가 방전에서 충전으로 바뀔경우 아래쪽에서 위쪽으로 순식간에 뛰어오른다
- SoC에 따라 선형적으로 Hysteresis Voltage를 변화시키는 Model이 필요
참고 자료 :
[ Math ] Convolution(합성곱)의 원리와 목적
[ Math ] Convolution(합성곱)의 원리와 목적 Convolution Convolution (합성곱) 많이들 들어 보셨을 겁니다. 의미적으로는 두 함수를 서로 곱해서 합한다는 것이지요. 합성곱을 공부하셨다면 아래의 질문을
supermemi.tistory.com
728x90
반응형
'Research_SOC Estimation' 카테고리의 다른 글
| Estimating Battery`s SoC using Extended Kalman Filter (0) | 2024.05.29 |
|---|---|
| SOC Estimator Simulation by Matlab_LFP (0) | 2024.03.19 |
| About EIS, Randles Circuit, Warburg Impedence (0) | 2024.03.07 |
| Estimation of SOC by Amphere Counting(전류적산법), OCV(Open Circuit Voltage) and EKF(Extended Kalman Filter) (0) | 2023.12.27 |



