Estimating Battery`s SoC using Extended Kalman Filter

- Kalman Filter / Extended Kalman Filter 관련 상세 내용

• Kalman Filter 관련 상세 내용 : https://youngseong.tistory.com/242

Kalman Filter란

 

• Extended Kalman Filter 관련 상세 내용 : https://youngseong.tistory.com/247

Extended Kalman Filter란

 

0. 목표

• EKF를 통한 SOC Estimator 구현
• Matlab 상에서 Estimator Simulation을 통한 평가
• 단 Cell 대상

 

1. Equivalent Circuit Model

• 아래와 같은 방전 전류 인가에 따른 Cell의 전압 반응을 Thevenin Equivalent Circuit으로 모사

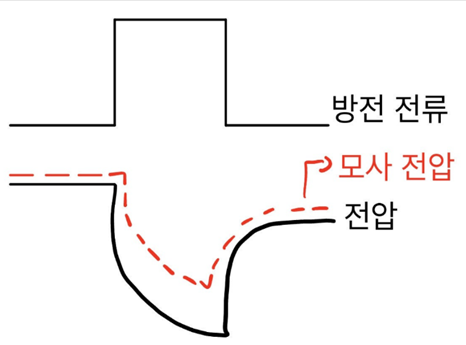
• 즉 Cell의 전기화학적 반응을 디지털 회로로 모사

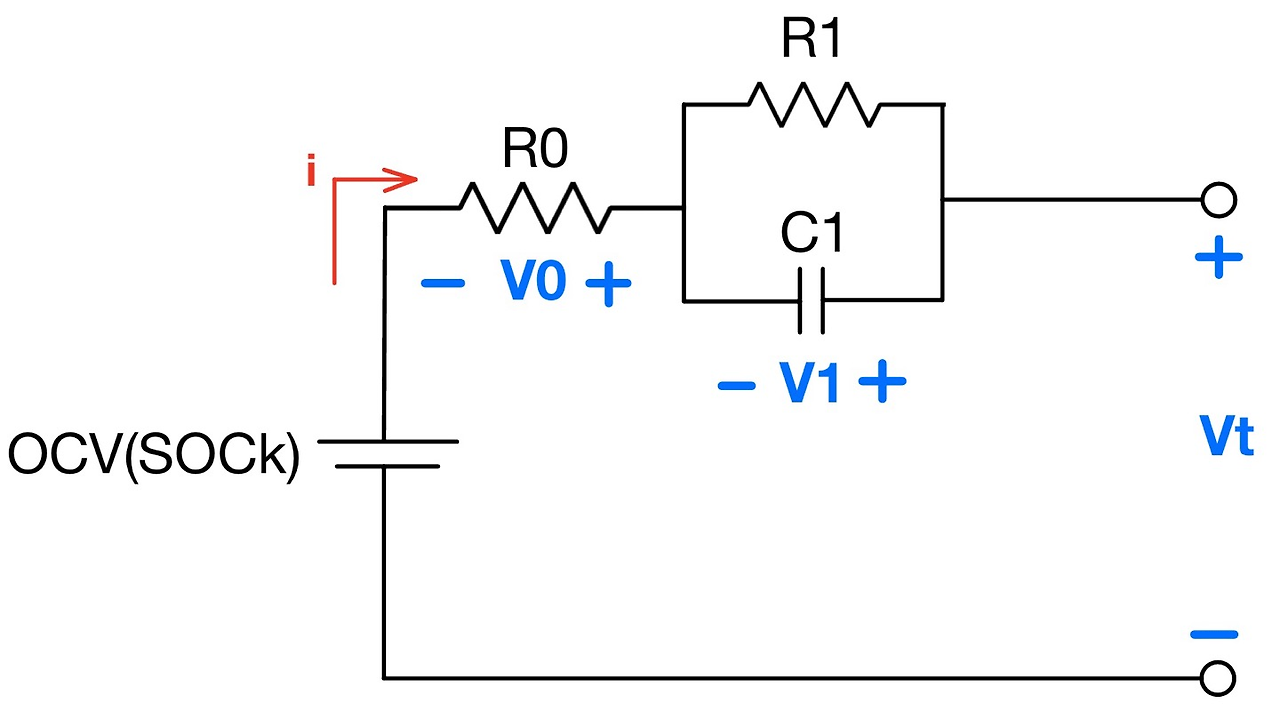
• 1차 RC 회로
• 각 소자들의 의미는 아래와 같으며, 모두 실험을 통해 구해야 한다
• OCV(SOCk) : OCV - SOC Look Up Table을 통해 충전량에 따라 변화하는 Cell의 단자 전압 표현

OCV-SOC Lookup Table 예시

• R0 : 방전 전류 인가에 의한 순간적인 전압 강하 표현 (빨간색 원)
• R1 - C1 : 이후로의 비선형적인 전압 강하 표현 (파란색 원)

방전 전류에 대한 Cell의 전압 응답

 

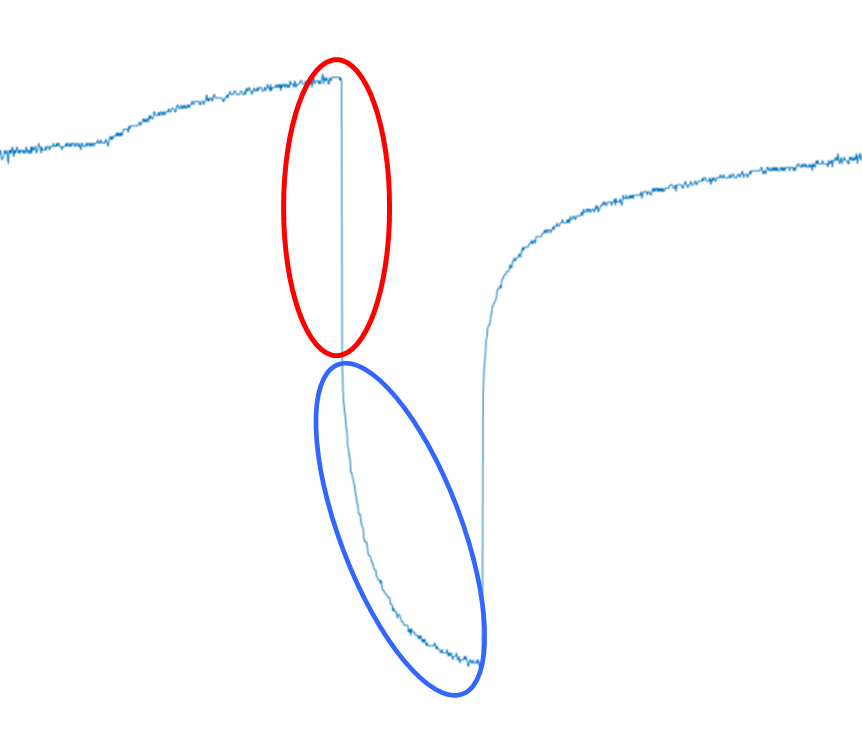
• 위처럼 RC Ladder의 갯수가 많아질수록 위 전압의 과도응답 부분이 더 세분화되어 잘 반영됨
  • 즉 동적 특성이 향상
• 단 RC Ladder가 많아질 수록 State가 늘어나 수식이 복잡해져 계산량이 증가한다
  • 따라서 이를 무한히 늘릴 수는 없다
• 적용 Application에 적합한 RC Ladder 갯수를 선택해야 함

 

1.1 ECM Parameter 도출

• 실험을 통해 ECM Parameter 선정

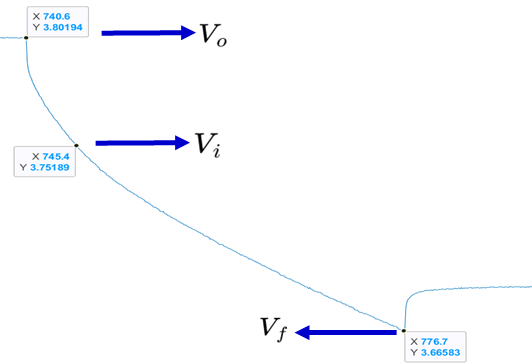
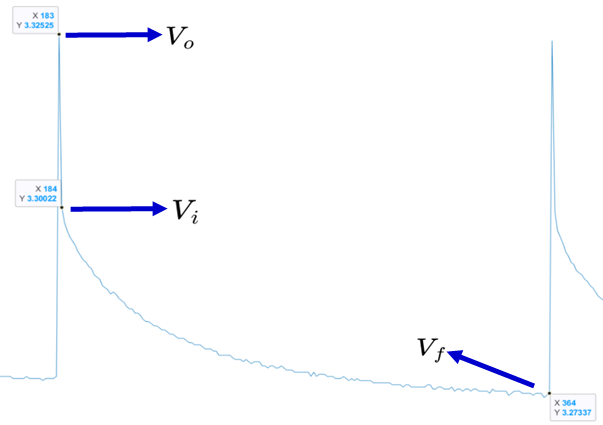
• 대상 Cell에 반복적으로 방전 전류를 인가한 후 위와 같이 Vi, Vo, Vf 지점 도출
• Vo : 방전 전류 인가 직전의 전압
• Vi : 방전 전류 인가 후 시정수(𝛕)까지의 전압
  • 𝛕(시정수) : Vo - Vf 사이의 63.2%에 도달했을 때의 시간  
  • 시정수 : 인가된 신호의 63.2%에 도달하는데 걸리는 시간
• Vf : 방전 전류 제거 직후의 전압
  
  • V0은 R0에, V1은 RC Ladder에 걸리는 전압

 

• 이후 위의 수식을 통해 ECM Parameter 계산
• 이후 단자 전압 예측 결과를 확인하며 실험적으로 Parameter 값 수정
  • i : 방전 전류

 

• ECM 수식 유도 관련 상세 내용 : https://youngseong.tistory.com/317

Battery Modeling by Equivalent Circuit Model

 

 

2. State Space Equation 구성

• ECM의 State Space Equation 구성
• Cell의 충/방전 실험 과정에서 얻을 수 있는 Cell의 Data는 총 3개
  1. Cell의 단자 전압 Vt
  2. 방전 전류 ik
  3. 온도 T

• 이 중 ik를 ECM의 입력으로, Vt를 출력으로 설정
• SoC와 RC 병렬 구조의 전압 V1을 State Variable로 지정

 

• State Space Equation 관련 상세 내용 : https://youngseong.tistory.com/244

About State Space Equation

 

2.1 State Equation 구성

• 각 State Variable의 시간에 따른 변화를 수식으로 정리

SoC 관련 수식

• 위 SoC 관련 수식은 전류적산법 수식과 동일

 

V1 관련 수식

 

System Matrix

• 두 방정식을 하나의 System Matrix로 정리
• 위 Matrix에는 Non Linear 성분이 포함되어 있음
• 이를 Extended Kalman Filter에 활용하려면 Linear Equation 형태로의 Linearization 필요

 

SOC와 전류의 관계는 선형성을 보이나 SOC와 전압 관계는 비선형성을 나타냄

 

 

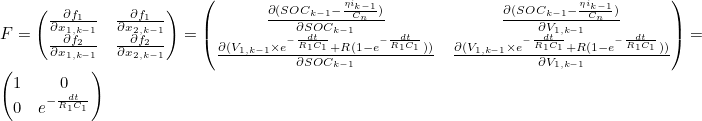
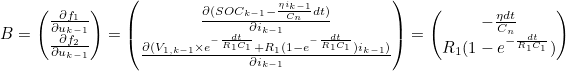
• u는 Cell에 입력되는 전류를 의미

 

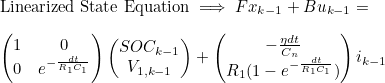
• System Matrix의 State Variable과 Input Variable에 대한 Jacobian Matrix 계산을 통해 Linearization 진행

 

2.2 Measurement Equation 구성

• KVL(Kirchhoff`s Voltage Law)를 통해 ECM의 입출력 관계식 구성

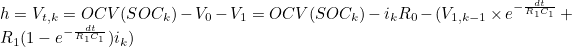
• 마찬가지로 이를 Extended Kalman Filter에 사용 가능한 Linear Equation 형태로 Linearization 필요

 

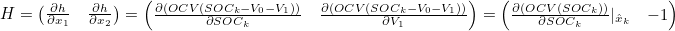
• 입출력 관계식의 State Variable에 대한 Jacobian Matrix 계산을 통해 Linearzation 진행

 

3. Extended Kalman Filter

3.1 전체 과정

 

 

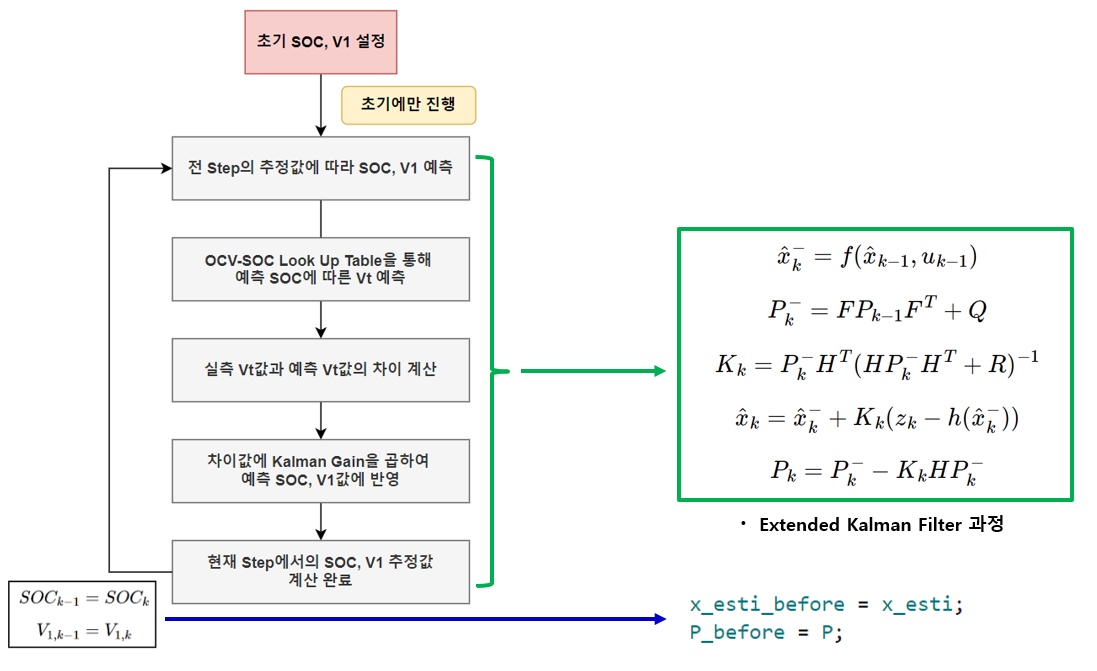
3.2 상세 과정  (NCM Cell SOC 100% 0 -> 0% 방전 과정)

State Equation

 

Measurement Equation

 

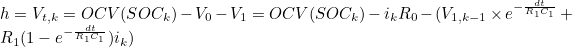
0. 초기값 지정

- 아래 값들은 설명을 위한 예시 값

초기 상태변수 값 (SoC, V1) 선정

 

초기 오차 공분산 설정

 

System Noise Covariance 설정

 

Sensor Noise Covariance 설정

 

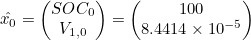
• ECM은 실제 Cell을 매우 유사하게 모사하고, 전류 측정에 큰 Noise가 있다고 가정

1. Prediction Step

• State Equation을 통해 추정 현재 시점에서의 상태변수 예측 

 

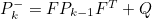
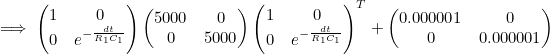
• 오차 공분산 예측

2. Update Step

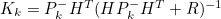
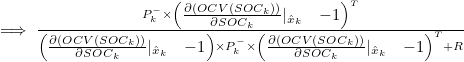
• Kalman Gain Update

 

 

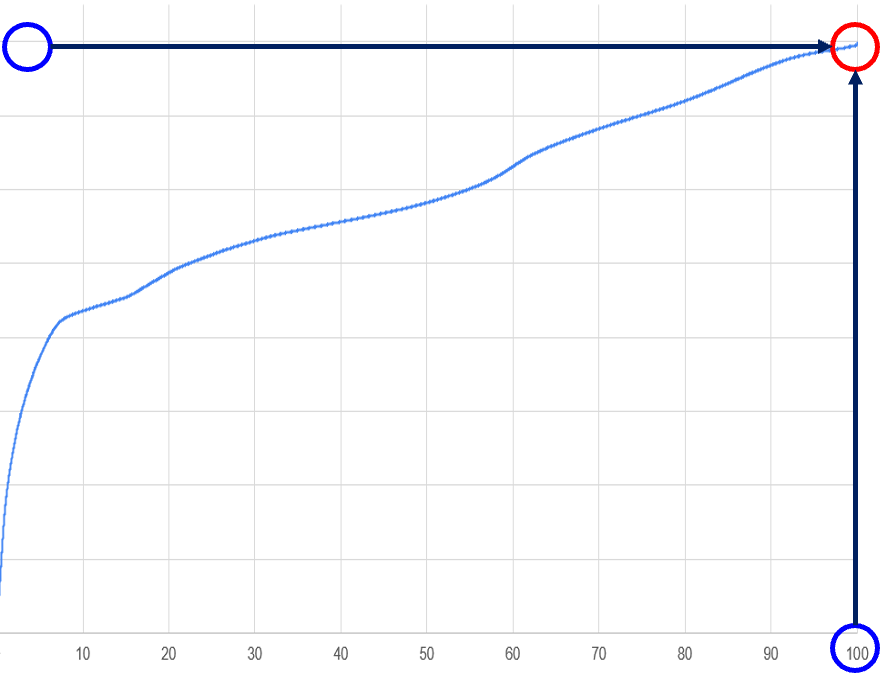
• 예측 State Variable 중 SOC 값을 OCV-SOC Look Up Table에 적용시켜 해당 SOC에 해당하는 전압값(OCV) 취득

 

• 이 OCV를 ECM의 입력으로 사용
• 이후 Measurement Equation을 통해 R0, R1-C1 병렬 구조를 통과한 후의 출력 전압 Vt 계산
  • 이 Vt 계산값이 예측 단자 전압 값

 

• 측정값 (Vt, 단자 전압)을 통한 상태변수 추정값 Update
  • 위에서 구한 예측 Vt와 실측 Vt를 비교
  • 둘의 차이값을 Kalman Gain에 곱한 값을 예측 상태변수값에 더함
  • 위 과정을 통해 예측 State Variable 값을 추정 State Variable값으로 Update

실측 단자 전압

 

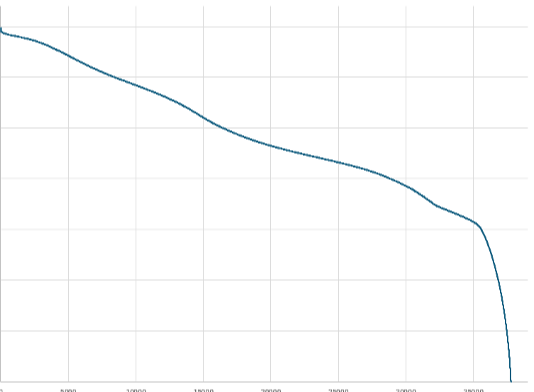
• 이 추정 State Variable 값이 EKF를 통해 구하고자 하는 현재 시점의 SOC 값

 

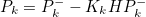
• 추정 상태변수의 오차 공분산 Update

 

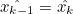
• 위에서 구한 추정 State Variable 값은 다음 시점에서 이전 시점의 추정 값으로 쓰임

 

위 과정을 재귀적으로 반복하며 SOC를 추정

 

 

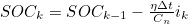
• 이를 위의 전류적산법 기반의 SOC 추정과 비교

 

4. Matlab Simulation

4.1 Simulation 과정

• SOC 100% - 0% 간의 연속적인 충 / 방전 과정에서의 SOC를 추정

 

4.2 Matlab Simulation 구조

• Simulation 대상 Cell 정보 초기화, 실험 Data 인가, EKF 과정 등을 함수로 각각 분리
• 지정한 Sampling Time 간격으로 총 k번의 SOC 추정 진행
• 인가 전류값에 일정한 간격의 Random Noise 추가
• SOC 추정 완료 후 RMSE를 통한 전류적산법과 EKF의 정확도 비교

 

4.3 Simulation 결과

• ECM Parameter 및 EKF Parameter를 지속적으로 Tuning해가며 Simulation 진행

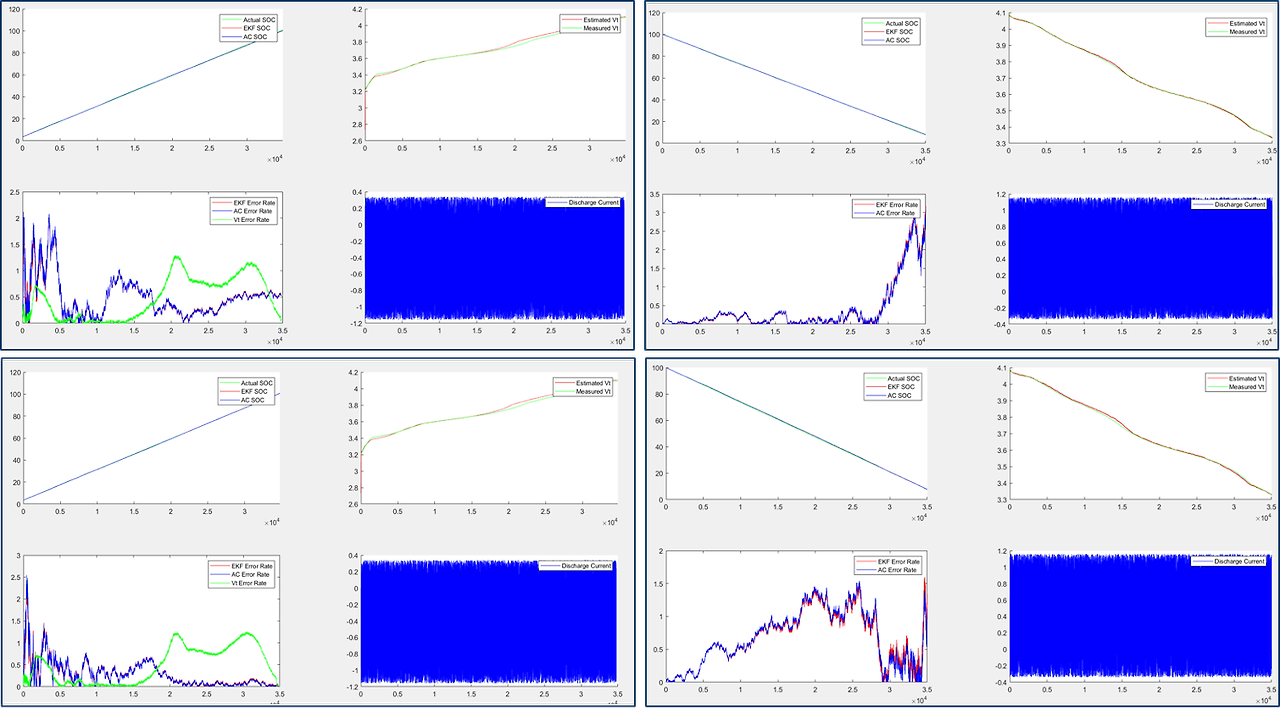
• 왼쪽 위 : 실제 SOC, 전류적산법 / EKF 기반 추정 SOC
• 오른쪽 위 : 예측 단자 전압, 측정 단자 전압
• 왼쪽 아래 : 전류적산법 / EKF 기반 SOC 추정 오차율, 단자 전압 예측 오차율
• 오른쪽 아래 : 인가 전류

 

• 이후 전류적산법과 EKF의 SOC 추정값 RMSE 비교
  • RMSE_difference 값이 0 이상이면 EKF의 SOC 추정 성능이 더 우세함을 의미

 

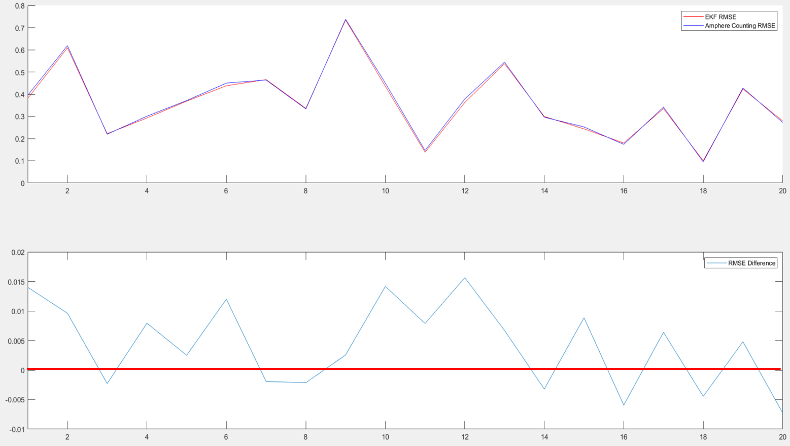
• 충 / 방전 간의 SOC 추정 RMSE 비교

 

4.4 Source Code

• Matlab Source Code : https://github.com/YoungSeong98/SOC_Estimatior_Simulation_by_Matlab

GitHub - YoungSeong98/SOC_Estimatior_Simulation_by_Matlab

 

5. Kalman Filter 기반 SoC 추정의 어려움

5.1 이론 관련

• 제어 이론을 기본으로 Battery에 적용시켜야 하며, 실험 기반의 Data가 바탕이 되어야 함
  • 쉽지 않은 제어 이론
  • 실험 Data를 얻는데 상당한 시간이 소요됨
• 또한 Module, Pack 레벨에선 Cell 간의 편차가 존재하여 이를 위한 편차 Model이 추가적으로 들어가야 함
  • 이로 인해 방법론이 복잡해짐
• 따라서 단순히 EKF를 적용하기 보다는 구간에 따른 여러 방법론을 추가하는 등의 적용이필요
  • Ex) 전압 변화율이 큰 SoC 구간에는 EKF 적용 / 작은 구간에는 전류적산법 적용

 

5.2 LFP 관련

LFP Cell의 OCV-SoC Lookup Table. 출처 : https://www.researchgate.net/figure/Experimental-OCV-SOC-curve-for-LiFePO4-battery-cell-under-testing_fig2_273161090

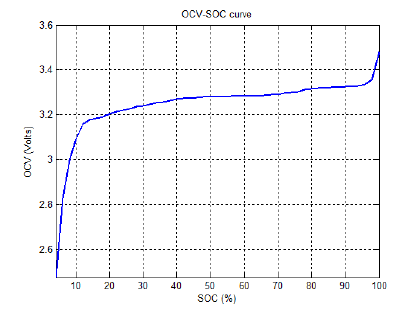
• LFP Cell의 경우 위처럼 SoC에 대한 OCV의 변동의 폭이 매우 적은 구간이 있다
  • 따라서 측정 전압에 대한 정밀도가 요구
• 이처럼 SoC가 변해도 OCV가 크게 변하지 않는 이유는 분자의 변화가 거의 없기 때문

 

 

• 이러한 특성을 가진 LFP Cell의 SoC를 추정할 경우, 정밀도 향상을 위한 여러가지 방법이 있다

 

5.2.1 해결책

1. 충 / 방전 OCV 구분

• OCV는 기본적으로 방전 과정에서 얻어지나, LFP의 경우 충/방전 OCV가 달라 이를 구분지어야 함

 

2. Major / Minor Loop 구분

충 / 방전 OCV 사이의 Major / Minor Loop

• Major Loop는 전체적인 틀, Minor Loop는 내부에서 Mode가 바뀌는 부분

 

3. Hysteresis 특성 반영

• Hysteresis 특성 : 어떤 물리량이 그 값 전까지 해당 물질이 경과해온 과정에 따라 달라지는 특성

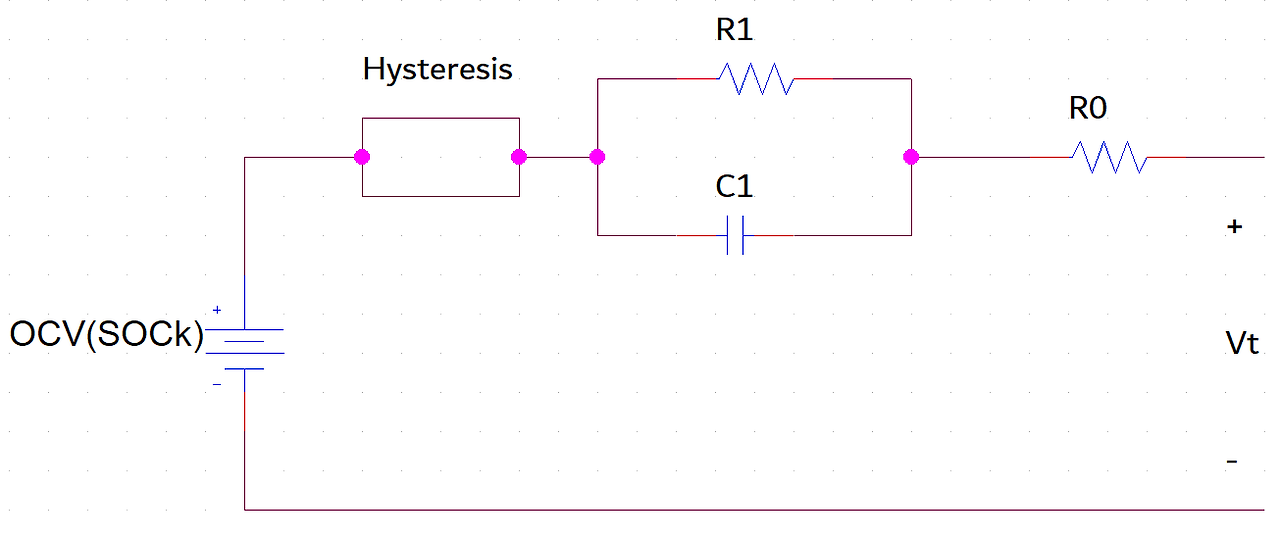
• 아래처럼 Hysteresis 요소를 ECM에 추가하여 Hysteresis 특성을 반영할 수 있다

 

4. 노화 반영

가로축이 시간, 세로축이 전압

• Battery 노화 시 OCV - SoC 커브의 특성이 위와 같이 바뀜
• 즉 Upper / Lower Cutoff Voltage는 그대로이나 거기까지 도달하는 소요 시간이 짧아짐
  • 이로 인해 Battery Capacity 감소

• LFP의 경우 노화에 따라 OCV - SOC LUT에 변화가 생기는 경우가 많아 노화에 따라 OCV를 구분하는 것이 일반적
  • 단 LFP는 비선형 특성이 너무 많아 실험을 통해 OCV - SOC 커브 변화의 요인이 노화때문인지를 판단해야 함
  • 전류 / 온도 등에 의해 변화가 생길 수도 있음

온도 별 전압-용량 곡선. 출처 : https://battengineer.co.kr/soc-state-of-charge/

• 온도에 따라 용량이 감소하는 모습