1. Unscented Kalman Filter란
- Extended Kalman Filter처럼 Non Linear System을 Kalman Filter에 적용시키는 방법 중 하나
- 즉 Gaussian Distribution이 입력으로 들어올 때 출력 또한 Gaussian Distribution 형태로 얻는 방법
- 원래의 함수 x값을 대표할 수 있다고 여겨지는 몇 점들을 Non Linear Function에 대입시켜 새 차원의 평균, 분산을 알아내는 방식
- 비선형함수 f(x)에 점들을 하나하나 대입하여 어떤 함수가 나오는지 대략적으로 확인하는 것
2. Extended Kalman Filter와의 차이점
- Non Linear Function을 매 Step마다 Linearization하는 EKF와는 달리 Non Linear Function 자체를 알아내는 방식
- EKF는 System의 Nonlinearity가 매우 클 경우, 평균과 공분산이 Non Linear Model의 Linearization을 통해 전달되었으므로 추정 성능이 매우 저하될 수 있다
- Linear System의 경우 EKF와 UKF는 동일한 결과값을 갖는다
- Non Linear System에서는 UKF가 EKF보다 더 정확한 근사화 결과를 보인다
- 단 큰 차이를 보이진 않는다
- UKF는 Jacobian matrix를 구할 필요가 없다
- Linearization 과정이 없기 때문
- 계산 복잡도는 비슷하며, 계산 속도는 UKF가 EKF에 비해 조금 더 오래 걸린다
1) EKF

- EKF는 기존 Gaussian Distribution의 Mean 값 주변에서 Linearization을 진행
- Non Linear System을 1차 Taylor Series를 통해 근사화한 후 Jacobian Matrix 계산을 통해 System Model에 대한 Linearization 진행
- 이후 Linear Kalman Filter와 동일한 과정 수행
- 즉 Gaussian Distribution 근사화를 위해 Mean 값 하나만을 사용함
2) UKF

- UKF는 Non Linear System을 대표할 수 있는 여러 점들을 선정 후 Non Linear Function에 대입
- 이 결과값들의 Mean, Covariance 값을 계산해 새 Gaussian Distribution을 구함
- 즉 Gaussian Distribution 근사화에 다수의 점들을 사용함
- 이 점들을 'Sigma Point' 라고 함
- EKF가 사용하는 Mean값 근처에서의 Linearizaiton을 피하기 위한 방법
- 다수의 점들을 사용하므로 EKF에 비해 연산량이 많음
- EKF는 계산 시간, UKF는 정확도 면에서 강점을 보임
- Linearization 과정이 없으므로 Jacobian 계산을 필요로 하지 않음
3. UKF 정리
- 즉 x 값을 대표할 수 있는 몇 개의 점(xk)들을 Non Linear Function f(x)에 대입하여 f(xk)의 모습을 유추하는 방식
- 위 과정을 'Unscented Transform' 이라 함
- 이 Sigma Point는 많을수록 좋으나 그만큼 계산량이 늘어나므로, 적절한 수를 선정해야 함
- Unscented Transform의 과정은 아래와 같다
- Sigma Point Set 계산
- 각 Sigma Point에 Weight 부여
- Non Linear Function을 통해 점들을 Transform
- Weight가 부여된, Transform된 점들을 통해 Gaussian Distribution 계산
- 새 Gaussian Distribution의 Mean, Variance 계산
- Mean 값에서 멀리 떨어진 Sigma Point일수록 Weight을 낮게 주고, 가까울수록 높게 줘 원래의 Gaussian Distribution의 형태가 잘 유지되도록 함
- Weight 값은 Gaussian Distribution을 다시 계산할 때 사용된다
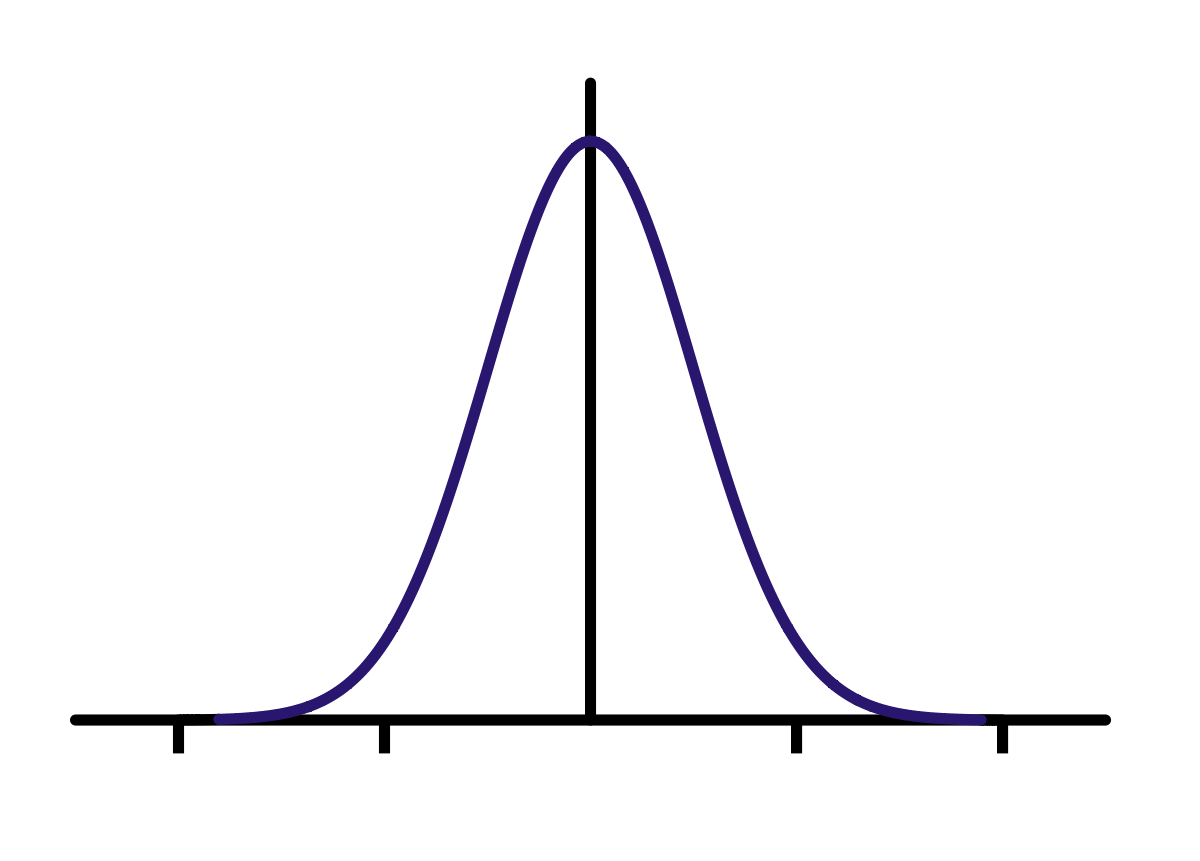
- xk 또한 Gaussian Distribution을 가짐
- 위 Mean(평균) 값을 기준으로 Standard Deviation(표준 편차. Variance(분산)의 제곱)만큼 떨어진 값들을 Sigma Point로 잡음
- Mean 값에서 멀리 떨어질수록 Weight를 낮게 주고, 가까울수록 Weight를 높게 줌
- 이를 통해 원래 xk 값에서의 Gaussian Distribution 형태가 잘 보존되도록 Sigma Point를 선정함
- 즉 Standard Deivation과 Mean값을 통해 해당 함수를 대표할 수 있는 점인 Sigma Point들을 찍고 함수 f(x)에 대입하여 새로운 f(xk)의 Mean, Variance 값을 구해주는 원리
- 즉 평균 주변에 Sampling Point (Sigma Point)의 최소 집합을 얻는 방식
- Sigma Point가 많을수록 원 함수에 가까운 함수를 얻을 수 있으나 연산량이 많아짐
- Sigma Point는 Weight 값, 즉 가중치가 붙음
- 이를 'Weighted Sigma Points'라 부픔
- UKF는 위의 변환된 점들에 대한 Mean 값과 Covariance를 계산하여 새로운 Gaussian Distribution을 만드는 것이 목표인 Filter
- Monte Carlo Sampling이나 예측 통계의 Taylor Series Expansion을 통해 수정 될 수 있다
4. UKF 동작 과정
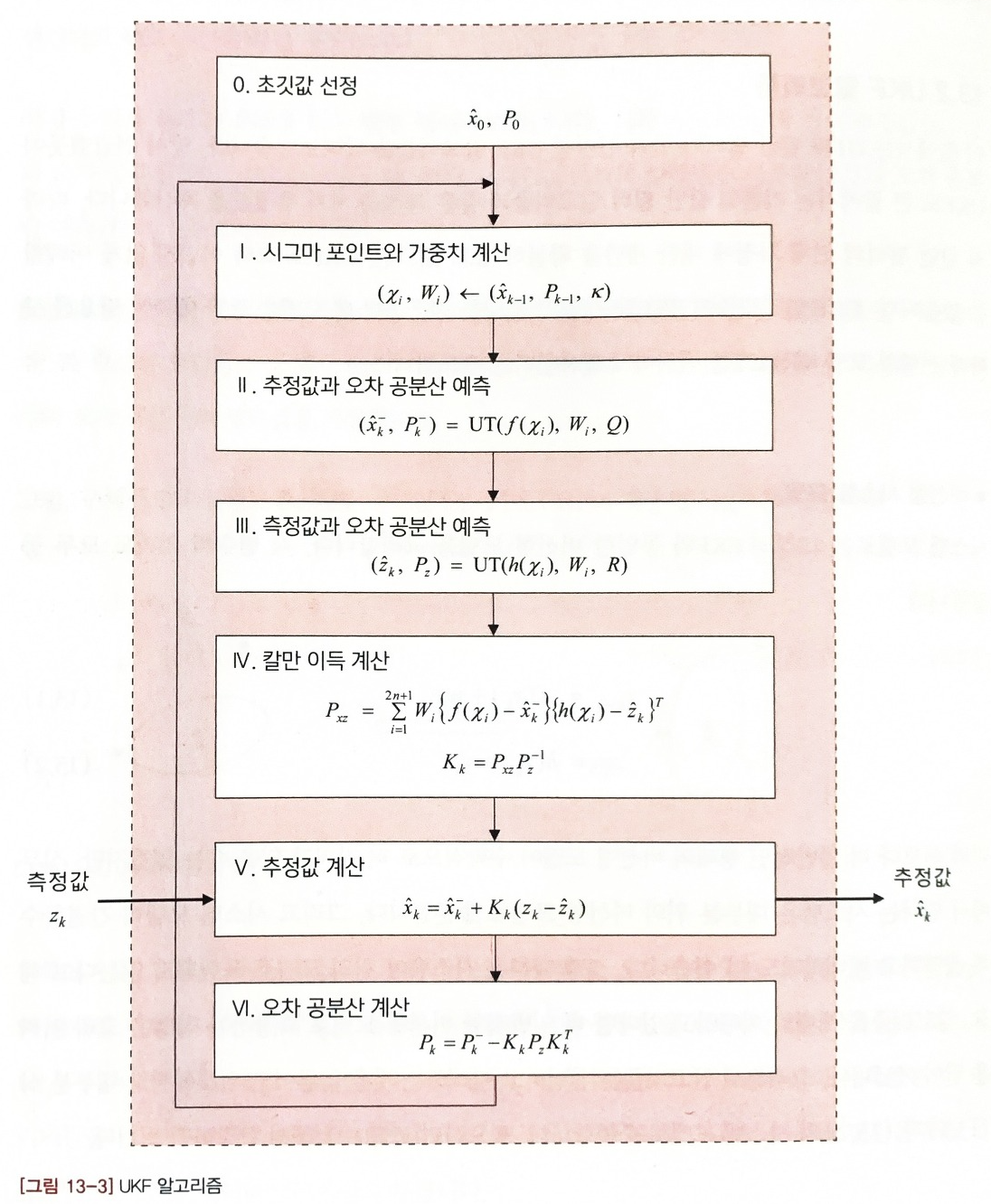
- UKF의 Predict Step은 앞서 다룬 Unscented Transform과 매우 유사하다
1) Sigma Point 선정
- Sigma Point의 수는 System의 Dimentionality에 따라 달라짐
- 보통 2n+1개가 최적의 개수
- 일반적인 수식은 아래와 같다
$$ \chi^{0}=\mu $$
- 첫번째 Sigma Point는 Mean Vector
$$ \chi^{i}=\mu +(\sqrt{n+\lambda}\Sigma)_{i}\implies i=1,\ldots $$
$$ \chi^{i}=\mu -(\sqrt{n+\lambda}\Sigma)_{i-n}\implies i=n+1,\ldots 2n $$
- χ : Sigma Point Matrix
- 이 Matrix의 모든 열은 Sigma Point를 나타냄 (System이 2차원이라면 Matrix는 2 x 5 형태가 됨)
- 각 Dimension마다 5개의 Sigma Point들이 있음
- 이후 2n개 만큼의 Sigma Points 추가
- μ : Gaussian Distribution의 평균
- n : System의 Dimentionality
- λ : Scaling Factor
- Mean 값으로부터 얼마나 떨어진 점을 Sigma Point로 잡아야 할지를 나타냄
- 3-n 이 최적의 값
- Sigma Point 중 하나는 Mean 값이고, 나머지는 위의 수식을 통해 구함
- Σ : Covariance Matrix
- 어떤 Matrix S가 아래 조건을 만족할 경우
$$ \Sigma=S*Sor\Sigma=S.S^{T} $$
- Matrix에 대한 Square가 성립됨 : Matrix Square Root
$$ S=\sqrt{\Sigma} $$
- 이 Matrix Square Root는 Eigen Value Decomposition, Cholesky Factorization 총 2가지 방법으로 구할 수 있다
1. Eigen Value Decomposition
- Covariance Matrix는 정방행렬이므로, Eigen Value Decomposition을 통해 아래와 같이 표현할 수 있다

- D Matrix는 Σ의 Eigen Value를 Diagonal 값으로 갖는 Matrix이다
- 따라서 S는 아래와 같이 나타낼 수 있다
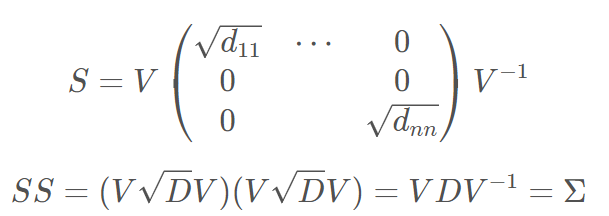
2. Cholesky Factorization
- Cholesky Factorization는 Matrix A가 Symmetric Matrix이고 Positive Definite할 때 Lower Triangular Matrix L 의 LL^T 로 분해하는 방법이다
- 위 방법의 결과값이 더 안정적이여서 주로 이 방식을 사용한다
2) Sigma Point Weight 계산
$$ w^{0}=\frac{\lambda}{n+\lambda} $$
- Mean 값에 대한 Weight 계산
$$ w_{c}^{0}=w_{m}^{0}+(1-\alpha^{2}+\beta) $$
- Covariance에 대한 Weight 계산
$$ w^{i}=\frac{1}{2(n+\lambda)}\implies i=1,\ldots,2n $$
- 모든 Weight 값의 합은 1이 되어야 한다
3) 근사 Gaussian Distribution의 Mean, Covariance 예측
$$ \mu'=\sum_{i=0}^{2n}w^{i}g(\chi^{i}) $$
- Mean 값 예측
- g : Non Linear Function
$$ \Sigma'=\sum_{i=0}^{2n}w^{i}(g(\chi^{i})-\mu')(g(\chi^{i})-\mu')^{T} $$
- Covariance 값 예측
1. Prediction Step
1-1 Sigma Point 선정
$$ \chi^{0}=\mu $$
$$ \chi^{i}=\mu +(\sqrt{n+\lambda\Sigma})_{i}\implies i=1,\ldots ,n $$
$$ \chi^{i}=\mu -(\sqrt{n+\lambda\Sigma})_{i-n}\implies i=n+1,\ldots,2n $$
- 첫번째 줄은 Mean Vector
- 두번째 줄은 Covariance Vector
- 세번째 줄은 나머지 Sigma Points (2n개의 Sigma Points 추가)
- 전체 Sigma Points는 2n + 1(Mean)
- χ : Sigma Point Matrix
- 이 Matrix의 모든 열은 Sigma Point를 나타냄 (System이 2D라면 2x5 형태가 됨)
- 각 Dimension마다 5개의 Sigma Point를 가짐
- μ : Gaussian Distribution의 평균
- n : System의 Dimentionality
- λ : Scaling Factor
- Mean 값으로부터 얼마나 떨어진 점을 Sigma Point로 잡아야 할지를 나타냄
- 3-n 이 최적의 값
- Σ : Covariance Matrix
1-2 Sigma Points Weight 계산
$$ w^{0}_{m}=\frac{\lambda}{n+\lambda} $$
$$ w^{0}_{c}=w^{0}_{m}+(1-\alpha^{2}+\beta) $$
$$ w^{i}=\frac{1}{2(n+\lambda)}\implies i=1,\ldots,2n $$
- 첫번째 줄은 Mean 값에 대한 Weght
- 두번째 줄은 Covariance에 대한 Weight
- 세번째 줄은 나머지 Sigma Point들에 대한 Weight
- 이 Weight 값들은 Gaussian Distribution을 다시 계산할 때 사용됨
1-3 Gaussian Distribution 계산
$$ \mu'=\sum_{i=0}^{2n}w^{i}g(\chi^{i}) $$
$$ \Sigma'=\sum_{i=0}^{2n}w^{i}(g(\chi^{i})-\mu')(g(\chi^{i})-\mu')^{T}+R_{t} $$
- 계산된 Sigma Point들을 Non Linear Function에 Input으로 넣고 Output을 통해 Gaussian Distribution 추정
- 기존의 Mean, Covariance 예측 식에 Process Noise R이 추가된 형태
2. Update Step
- Update Step 전 Sigma Point를 재계산할지 그냥 진행할지를 선택할 수 있다
- 본 예제의 경우는 그냥 진행하는 것을 선택
$$ \mathbb{Z}=h(\chi) $$
$$ \hat{z}=\sum_{i=0}^{2n}w^{i}\mathbb{Z}^{i} $$
$$ S=\sum_{i=0}^{2n}w^{i}(\mathbb{Z}^{i}- \hat{z})(\mathbb{Z}^{i}- \hat{z})^{T}+Q
$$
- State Space에서의 State를 Measurement State Space로 변환
- Z : Muasurement Space에서 Transform 된 Sigma Points
- z^ : Measurement Space에서의 Mean 값
- S : Measurement Space에서의 Coveriance
- Q : Noise
- h : Sigma Point들을 Measurement Space에 대응시키는 Function
- 즉 State Space를 Measurement Space로 변환해주는 Function
$$ T=\sum_{i=0}^{2n}w^{i}(\chi^{i}-\mu')(\mathbb{Z}^{i}-\hat{z})^{T} $$
$$ K=T.S^{-1} $$
- Kalman Gain 계산
- T : Cross Co-Relation Matrix between State Space and Predicted(Measurement) Space
- EKF의 H Matrix와 동일
- S : Predicted Covariance Matrix
- K : Kalman Gain
$$ \mu=\mu'+K(z-\hat{z}) $$
$$ \Sigma=(I-KT)\Sigma' $$
- 최종 Mean, Covariance 값 계산
- z : 실제 측정값

참고 자료 :
The Unscented Kalman Filter: Anything EKF can do I can do it better!
I have just completed my Term 2 of Udacity Self Driving Car Nanodegree. I wrote about Kalman Filter and Extended Kalman Filter. Today we…
towardsdatascience.com
https://limitsinx.tistory.com/80
[제어시스템공학-12] Unscented Kalman Filter(UKF,무향칼만필터) 개념
[제어시스템공학-1] Average Filter(평균필터) https://limitsinx.tistory.com/69 [제어시스템공학-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70 [제어시스템공학-3] Low Pass Filter(저주파 통과필터) h
limitsinx.tistory.com
https://limitsinx.tistory.com/81
[제어시스템공학-13] Unscented Kalman Filter(UKF,무향칼만필터) 구현
제어시스템공학-1] Average Filter(평균필터) https://limitsinx.tistory.com/69 [제어시스템공학-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70 [제어시스템공학-3] Low Pass Filter(저주파 통과필터) ht
limitsinx.tistory.com
https://jinyongjeong.github.io/2017/02/17/lec06_UKF/
[SLAM] Unscented Kalman Filter(UKF) · Jinyong
[SLAM] Unscented Kalman Filter(UKF) EKF와 다른 선형과 과정을 이용하는 UKF를 설명한다. 본 글은 University Freiburg의 Robot Mapping 강의를 바탕으로 이해하기 쉽도록 정리하려는 목적으로 작성되었습니다. 이전
jinyongjeong.github.io
여러 종류의 칼만필터(Family members of Kalman Filter)(UKF)
[SLAM] Kalman filter and EKF(Extended Kalman Filter) · Jinyong [SLAM] Kalman filter and EKF(Extended Kalman Filter) Kalman filter와 Extended Kalman filter에 대한 설명. 본 글은 University Freiburg의 Robot Mapping 강의를 바탕으로 이해하
jml-note.tistory.com
https://ko.wikipedia.org/wiki/%EC%B9%BC%EB%A7%8C_%ED%95%84%ED%84%B0
칼만 필터 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 칼만 필터(Kalman filter)는 잡음이 포함되어 있는 측정치를 바탕으로 선형 역학계의 상태를 추정하는 재귀 필터로, 루돌프 칼만이 개발하였다. 칼만 필터는 컴퓨
ko.wikipedia.org
https://blog.naver.com/ycpiglet/222139077774
[수학] 칼만 필터(Kalman Filter)란 무엇인가? (로봇, 자율주행, SLAM 알고리즘)
자율주행(Autonomous Driving)에는 기계(Mobility)가 이동을 하면서 스스로 장애물을 파악해서 피하고, ...
blog.naver.com
https://m.blog.naver.com/kaoara/221905928263
Positive Definite Matrix
- Positive Definite Matrix(정치행렬) : 고윳값이 양수인 Symmetric(대칭행렬)을 의미한다. Positive...
blog.naver.com
https://carstart.tistory.com/155
[선형대수학] 3. 콜레스키 분해(Cholesky decomposition), 대칭행렬, 정칙행렬
콜레스키 분해를 왜 사용하는가? 양정부호행렬을 하삼각행렬과 그 전치행렬의 곱으로 표현하는 것이다. 무슨말인지 어렵죠 ^^;; 하지만 콜레스키 분해는 계산상으로 매우중요합니다. 우선 LU분
carstart.tistory.com
촐레스키 분해(Cholesky decomposition)
1. 정의 행렬 A가 대칭행렬 일때 하삼각행렬과 상삼각행렬로 분해가 가능하다. A = LU (U = $L^T$) A = $LL^T$ 2. 방법 각 행렬 원소를 구하는 공식이 존재하며, 대각 원소를 구할 때와 그렇지 않을때가 구
dhpark1212.tistory.com
'Study_Engineering' 카테고리의 다른 글
| Thread란 (0) | 2024.07.09 |
|---|---|
| Nelder-Mead Algorithm 이란 (0) | 2024.05.03 |
| Extended Kalman Filter란 (0) | 2024.01.16 |
| Kalman Filter란 (0) | 2024.01.16 |
| 표준편차, 분산, 공분산 (0) | 2024.01.16 |



