0. 순서
1. Kalman Filter란
1.1 기본 개념
1.2 Kalman Filter 사용 이유
1.3 Kalman Filter 예시
2. Kalman Filter 동작 과정
2.1 전체 동작 과정
2.2 수식
2.3 상세 과정
2.3.1 System Model 관련
3. 관련 이론
3.1 Gaussian Distribution (정규 분포)
4. Kalman Filter 동작 원리
4.1 Example) 자율주행 Robot의 상태 추정
4.2 Kalman Filter Information Flow
1. Kalman Filter란
1.1 기본 개념
Kalman Filter : System을 어떤 Model로 모사한 후 그 Model을 통해 예측한 추정값과 실제 측정 데이터의 차이를 기반으로 오차 공분산을 이용해 System의 현재 상태를 추정하는 Algorithm
- Filter : 어떤 신호에서 Noise등의 원하지 않는 신호를 차단하거나, 원하는 신호만을 통과시키는 기능을 하는 회로 등의 장치나 과정
- 모든 Filter는 이전의 값이 현재 값에 영향을 주는 Recursive(재귀)적인 구조를 갖는다
- 기본적인 Filter들에 대한 예시
- https://youngseong.tistory.com/241
About Avg, MovAvg, LPF
Filter : 어떤 신호에서 원하지 않는 신호를 차단하거나, 원하는 신호만을 통과시키는 기능을 하는 회로 등의 장치나 과정 신호 처리의 일부로, 특정 Frequency를 차단 혹은 통과시킨다 원하지 않는
youngseong.tistory.com
- Bayes Filter를 기반으로 이전 상태로부터 현재의 상태를 예측한 후 예측값과 실제 Sensor를 통해 얻은 측정값의 오차를 이용하여 보정을 진행
- Bayes Filter : 불확실성이 포함되어있는 과거의 정보로부터 현재 상태의 추정값을 계산하는 Algorithm
- Time Update(State Prediction) -> Measurement Update 의 과정이 재귀적으로 진행
- 두 확률변수의 사전확률과 사후 확률의 관계를 나타내는 Bayes Theorem을 기반으로 함
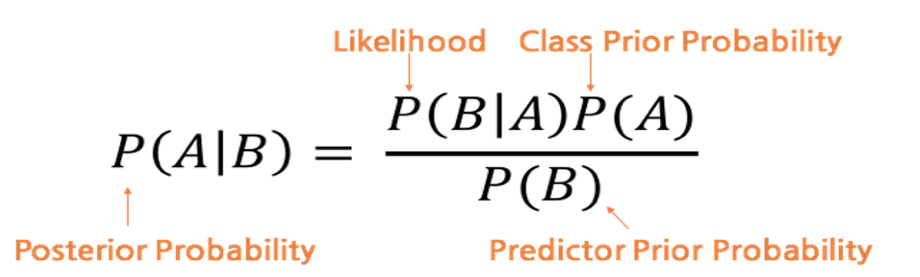
- Bayes Filter 식에서 모든 확률 분포와 Noise를 Gaussian Distribution으로 가정한 Model이 Kalman Filter
1.2 Kalman Filter 사용 이유
- 알고자 하는 변수를 직접 확인할 수 없어 간접적인 방법으로 유도하여 알아내야 할 때 사용
- Ex) 로켓 추진체 내부의 고온의 온도 측정
- 또는 Sensor를 통한 값 측정 시 측정값에 포함되어있는 Noise를 제거하기 위해 사용
Noise가 포함되어있는 측정값을 바탕으로 Linear System의 상태를 추정하는 Filter
1.3 Kalman Filter 예시
- Battery Modeling을 통한 SoC(State of Charge. 충전량) 추정
- 고열로 인해 내부의 SoC를 직접 측정할 수 없다 가정
- Battery를 Mathematical Model을 통해 표현하여 SOC 추정
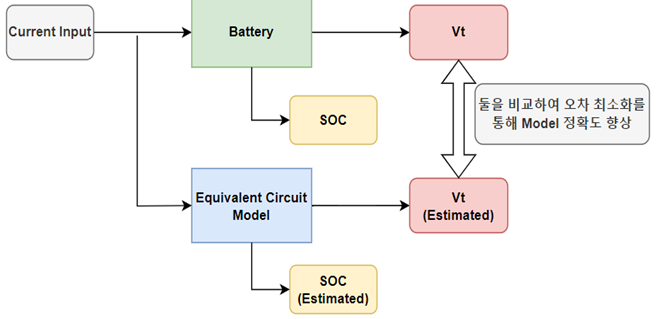

- Battery의 출력 전압 Vout을 직접 측정할 수 있을 경우, Battery의 실제 Vout과 Model을 통해 예측한 Vout값을 비교
- 그 오차율을 Model에 반영하여 오차값 최소화를 통해 추정 SoC 값의 정확도 향상 가능
- 위처럼 Kalman Filter는 System의 어떤 상태값과 Mathmetical Model을 통해 다른 상태값을 예측하는 State Observer 역할을 함
- 위의 경우 출력 전압을 통해 SoC를 예측
- Model의 예측값과 측정값의 차이를 기반으로 오차 공분산을 이용해 현재 상태를 추정
2. Kalman Filter 동작 과정
2.1 전체 동작 과정

- 초기값, 혹은 이전 Time Step에서의 추정값을 바탕으로 현재 Time Step에서의 추정값 예측
- 이를 Sensor를 통해 측정한 실제 측정값과 비교하여 현재 Time Step에서의 추정값 도출
- 예측 추정값을 보정
- 이 과정을 재귀적으로 반복
2.2 수식
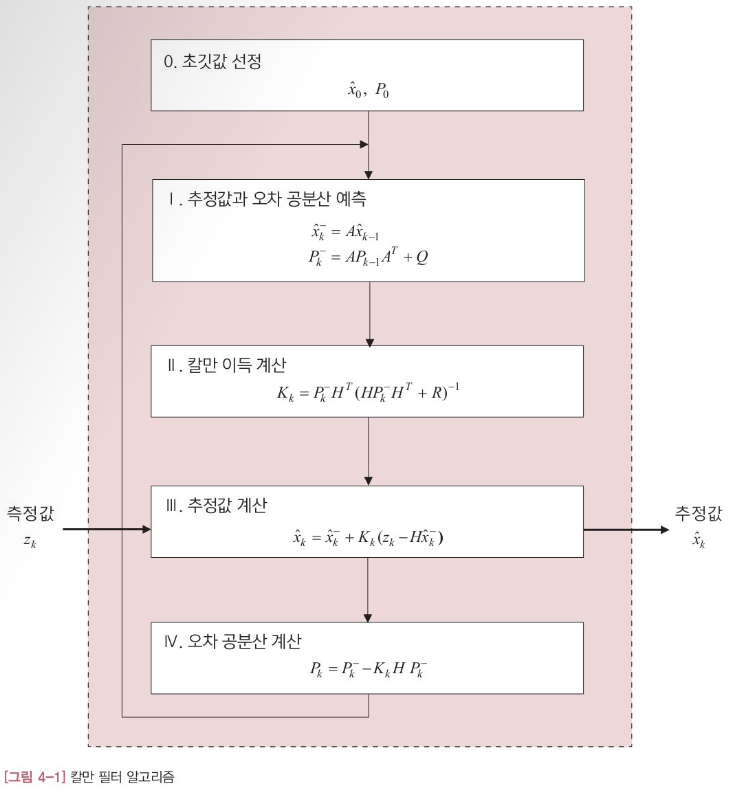
- 측정값 Zk가 입력으로 들어오면 내부에서 처리한 후 추정값 Xk를 출력
- 측정값 Zk를 Reference 값으로 삼고, Zk로 만들어진 State Equation의 다른 State Variable들을 지속적으로 구함
- 위 그림에서 '-'가 붙은 변수들은 예측값임을 의미
- k는 현재, k-1은 과거의 Time Step을 의미
- 위 수식에서 A, H, Q, R은 System Model Variable으로, Kalman Filter를 구현하기 전 미리 결정해야 하는 값
- 사용자가 조정할 수 있는 유일한 Variable들
이 System Model Variable들이 Kalman Fitler의 성능(정확도)에 중요한 영향을 미침
- 위 변수들은 System을 Modeling 할 때 사용된다
- 즉 System Model이 실제 Model에 가까워질 수록 성능이 향상됨
2.3 상세 과정
0) 사전 단계
- System의 물리/화학적 특성을 파악하여 System에 대한 State Space Equation 작성
- State Space Equation : System을 나타내는 다차 미분방정식을 다수의 1차 미분방정식으로 바꿔 Matrix로 표현한 것
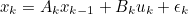

- xk : State Variable
- 차량의 속도, 배터리의 온도 등의 System의 상태를 나타내는 Variable
- u(t) : Input
- zk : Output 혹은 측정값
- Ak(System Matrix) : Input이 없을 때 시간에 따른 State의 변화를 나타냄
- Bk(Input Matrix) : Input에 따른 State의 변화를 나타냄
- Ck(Measurement Matrix) : 측정값과 State Variable 사이의 관계를 나타냄
- ϵt : Process Noise / δt : Sensor Noise
- 위 둘은 각각 평균이 0이고 Covariance (공분산)가 각각 R, Q인 확률 변수
- 관련 내용 : https://youngseong.tistory.com/244
About State Space Equation
State Space Equation : System을 나타내는 다차의 미분 방정식을 다수의 1차 미분방정식으로 바꿔 Matrix로 표현한 방정 확률론적 동적 System의 State Space 변화(한 Time Step에서 다음 Time Step에서의 State의 변
youngseong.tistory.com
1) 초기 State, Covariance 값 선정

- 처음의 State Variable x0과 그 Variable의 오차 Covariance P0을 예측하여 입력 (맨 처음 한번만 진행)
- Covariance (공분산) : 2개의 확률변수 간의 선형 관계를 나타내는 값. 추정값의 정확도를 보이는 역할
- 계산 결과값이 양수일 경우 서로 비례, 음수일 경우 서로 반비례 관계임을 의미
- 0일 경우 둘은 독립적인 관계임을 의미
- 추정 오차는 이 Covariance에 비례

- Variance(분산)은 확률변수 하나의 분포 상태, Covariance(공분산)는 두 확률변수 간의 선형관계를 나타냄
- 관련 내용 : https://youngseong.tistory.com/259
표준편차, 분산, 공분산
1. 표준 편차 (Standard Deviation) Mean(평균)에 대한 오차 범위를 나타냄 클수록 Data들이 퍼져있는 정도가 큼을 의미 단 아래처럼 데이터에 양수와 음수가 섞여있는 경우, 서로의 차이값이 상쇄되어 알
youngseong.tistory.com
2) 추정값, 오차 공분산 예측
전 Time Step에서의 결과값인 추정값과 오차 공분산 값을 통해 현재 Time Step에서의 추정값과 오차 공분산 예측
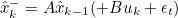
- State Variable 예측
- x^-k : 현재 Time Step에서의 State 예측값
- x^k-1 : 전 Time Step에서의 State 추정값
- 변수에 ' - '가 붙는 건 예측값이라는 의미
- A : 시간에 따른 System의 움직임을 나타내는 System Matrix
- 시간에 따른 상태의 변화를 야기하는 State Transistion Matrix (상태 천이 행렬)
- Kalman Filter 구현 시 이 A Matrix를 구하는 것이 가장 어려움
- B : Input이 State Variable에 미치는 영향을 표현
- B*uk : 외부에서 System에 영향을 주는 요인이 있을 경우 or Input에 의해 State Variable이 변할 경우 추가
- ϵt :Process Noise. System Model과 실제 System과의 차이를 반영
- Kalman Filter에서는 보통 Noise의 평균을 0으로 가정하므로 이렇게 명시적으로 계산할 일은 잘 없음

- 오차 공분산 예측
- Q : System Noise의 Covariance Matrix (Square Matrix)
- State 갯수와 같은 수의 행, 열을 가짐
- Kalman Filter는 System과 측정값의 Noise가 모두 Gaussian Distribution 형태를 갖는다고 가정
- System을 모사한 State Space Equation과 실제 System과의 오차를 나타냄
- External Uncertainty (외력)을 Noise로 표현한 후 그 Noise의 Covariance를 나타냄
- External Uncertainty : System이 의도한대로 동작하는 것을 방해하는 바람, 미끄러짐 등의 외력
- 즉 System의 정확한 상태 추정을 위해 매 Step마다 Uncertainty를 추가하여 Modeling에 표현
- 적절한 수치를 실험적으로 결정
- 전 Step의 State Variable을 알 때 현재 Step의 값을 얼마나 정확하게 예측할 수 있는지를 나타냄
- 따라서 Q Matrix는 System State Error Matrix P 계산에 들어간다
- 이 Q가 클수록 Sensor 측정값의 변화를 더 자세히 추적함
- 예측 Sensor 값보다 실제 Sensor 측정값을 더 신뢰한다는 뜻

* 예측(Predict)과 추정(Estimate)의 차이 : Low Pass Filter 와의 비교
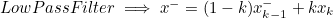
- 1차 Low Pass Filter의 경우 중간에 별도 과정 없이 새 추정값 계산에 직전 Step의 추정값(x-_k-1)을 사용
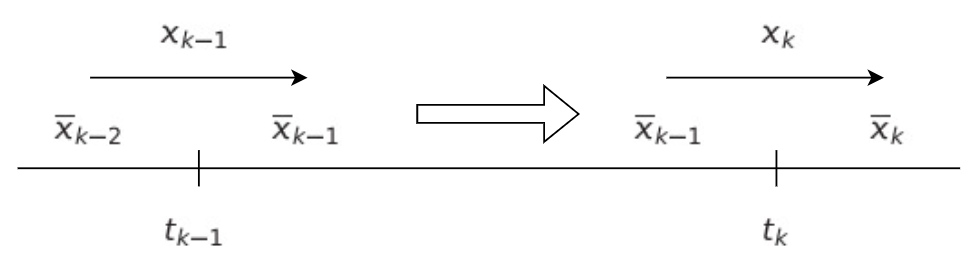

- 반면 Kalman Filter의 경우 직전 Step의 추정값 x^_k-1 대신 예측값 x^-_k 사용
- 아래처럼 예측값은 과정 I 에서 직전 Step의 추정값을 이용해 구한다

- 위 예측값을 추정 계산식에 대입하면

- 이처럼 Kalman Filter는 추정값 계산 시 직전 추정값을 바로 쓰지 않고 예측 단계를 한번 더 거침
- 따라서 예측값을 사전 추정값(Prior Estimate), 추정값을 사후 추정값(Posteriori Estimate)라고도 함
- 오차 공분산도 마찬가지

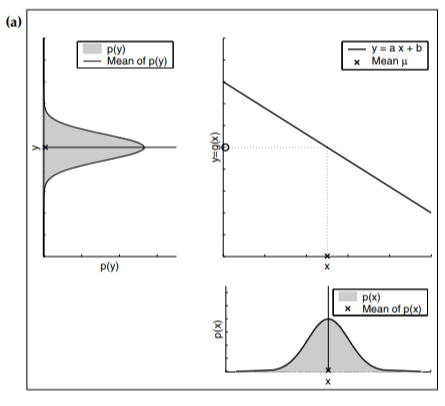
- 즉 이전 Step k-1 에서의 추정값이 (오른쪽 아래) System Model을 통과하여 현재 Step k에서의 Gaussian Distribution으로 계산된다
3) Kalman Gain 계산
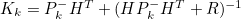
- 여기서 구한 Kalman Gain은 이후 추정값 계산 과정에서 예측값을 얼마나 보정할지 결정하는 Parameter 역할을 함
- K가 크면 추정값 계산에 측정값 반영 비율이 늘어남
- H : 측정값과 State Variable 사이의 관계를 나타내는 Output Matrix
- 측정값에 State Variable이 어떻게 반영되어있는지를 나타냄
- 예측 State 값을 예측 측정값으로 변환시킴
- State Space Equation의 C Matrix와 동일 역할
- R : Sensor Noise의 Covariance Matrix로, Noise를 Sensor에 반영 (Square Matrix)
- Sensor 측정값의 갯수와 같은 수의 행, 열을 가짐
- Sensor의 Datasheet를 참고하여 반영하거나 실험적으로 결정
4) 추정 State값 계산
위에서 구한 State 예측값, Kalman Gain, Sensor 측정값을 통해 현재 Time Step에서의 State값 추정
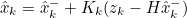
- Kk : Kalman Gain
- Zk : 측정값
- 위 식 중 아래의 항이 예측 측정값과 실제 측정값 간의 오차를 나타냄

- Hx-^k는 State 예측값을 H Matrix를 통해 예측 측정값으로 변환한다는 뜻

이처럼 Kalman Filter는 예측 측정값의 오차를 예측 State값에 반영하여 적절히 보상 후 최종 추정값을 계산함
5) 오차 공분산 계산

- 여기서 구한 P_k값은 다음 Time Step에서 P_k-1이 됨
- P_k : 예상값
- P-_k : 추정값
- K_k * H : 상수
- 정리
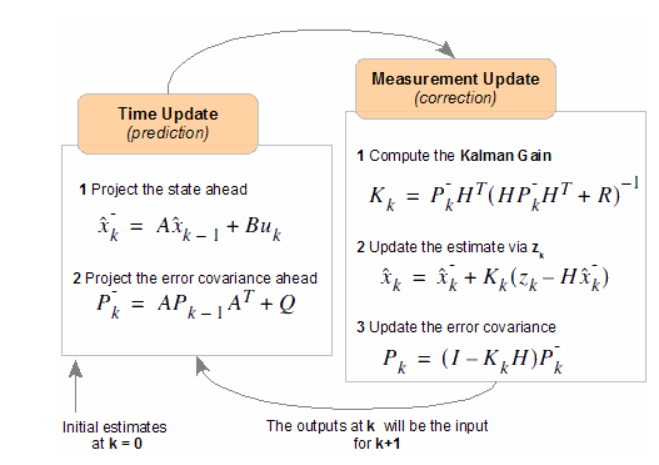
- 위 과정을 의미를 기준으로 분류하면 총 2단계로 나눌 수 있다
- 예측(Prediction) 과정 - 2단계
- 직전 Time Step에서의 추정값과 오차 공분산을 통해 예측값 출력
- A, Q System Model 변수 사용
- 현재 상태변수의 값과 정확도 예측
- 추정(Update) 과정 - 3~5 단계
- 예측 공분산 값을 통한 Kalman Gain 계산
- 예측 과정에서의 예측 상태변수 값을 통해 측정값을 예측
- 실제 측정값을 전달받아 예측 측정값과 비교하여 추정값과 오차 공분산 Update
- H, R System Model 변수 사용
- 즉 Kalman Filter의 동작 과정을 정리하면 아래와 같다
- System Model (A, Q)를 기반으로 다음 Step의 상태와 오차 공분산의 값 예측 : x^-_k, P-_k
- H Matrix를 통해 상태 예측값을 예측 측정값으로 변환
- 측정값과 예측 측정값의 차이에 Kalman Gain을 곱한 값을 예측 추정값에 더하여 추정값 Update : x^_k, P_k
- 위 과정을 반복
2.3.1 System Model Variable 관련
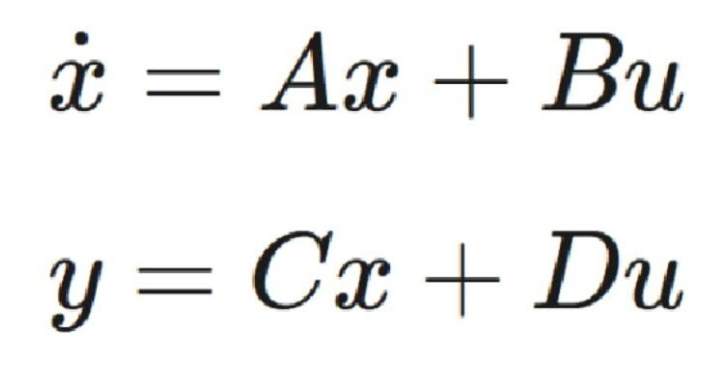
A, H : State Space Equation 성분
- 이 두 Matrix는 모든 성분이 상수이다
- A : 시간에 따른 System의 움직임을 나타내는 System Matrix로, State Transistion Matrix (상태 천이 행렬)로도 부름
- Input이 없을 때의 시간에 따른 State의 변화를 나타냄
- Kalman Filter 구현 시 설계가 가장 어려운 부분 (System에 대한 물리/수학적 이해 필요)
- k-1 -> k 로 넘어갈 때의 State 추정값의 Distribution 예측에 사용
- H : 측정값과 State Variable 사이의 관계를 나타내는 Output Matrix (State Space Equation의 C Matrix 역할)
- 측정값에 각 State Variable이 어떻게 반영되어있는지를 나타냄
- 예측 State 값을 예측 측정값으로 변환하는데 사용
Q, R : Noise 관련
- Kalman Filter는 System과 측정값에 모두 Gaussian Distribution을 갖는 Noise가 있다고 가정
- Q : System Noise의 Covariance Matrix로, System을 모사한 Model과 실제 System과의 오차를 반영
- External Uncertainty(외력)을 Noise로 표현한 후 그 Noise의 Covariance를 나타냄
- External Uncertainty : System이 의도한대로 동작하는 것을 방해하는 바람, 바닥 미끄러짐 등의 외력
- 즉 정확한 System의 정확한 상태 추적을 위해 매 Step마다 Uncertainty를 추가하여 Modeling에 표현


- 적절한 수치를 실험적으로 선정
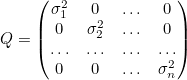
- R : Sensor Noise의 Covariance Matrix

- Sensor의 Datasheet를 참고하거나 실험적으로 선정
- Covariance의 Matrix는 위와 같이 변수의 분산들로 구성됨
- n개의 noise가 있고, 각 Noise의 분산이 σ1^2, σ2^2 ... σn^2 인 경우의 Covariance Matrix
- Kalman Filter 과정 중 Covariance Matrix 관련 부분
1) Kalman Gain 계산 식
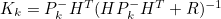
- 위 식의 모든 변수가 Scalar라 가정하면

- 위를 통해 R과 K는 서로 반비례관계임을 알 수 있다
- Kalman Gain이 감소하면 아래 식에 의해 추정값 계산에 측정값이 반영되는 비율이 작아짐
- 외부 측정값의 영향을 덜 받게 되어 추정값의 변화가 줄어듦

- 따라서 측정값의 영향을 덜 받고 변화가 완만한 추정값을 얻고 싶다면 Matrix R을 키우면 됨
2) 오차 Covariance 예측 식

- 위 식을 통해 Q와 P-_k는 서로 비례관계임을 알 수 있고, P-_k는 Kalman Gain K_k와 비례하므로 Q와 K_k는 비례한다
- Kalman Gain K_k가 증가하면 추정값 계산에 측정값의 반영 비율이 올라간다 (R과 반대)
- 따라서 측정값의 영향을 많이 받고 변화가 심한 추정값을 얻고 싶다면 Matrix Q를 키우면 됨
정리
- A, H : State Space Equation의 A, C Matrix
- Q, R : System / Sensor에 단순히 Noise 추가
- 둘 모두 Diagonal Matrix
3. 관련 이론
3.1 Gaussian Distribution (정규 분포)
- 상태 변수 x_k와 추정값(x^_k), 오차 공분산(P_k)은 아래와 같은 관계가 성립됨

- 이는 변수 x_k가 평균이 x^_k이고 공분산이 P_k인 정규분포를 따른다는 뜻
- P_k가 정규분포 그래프의 폭을 결정

Gaussian Distribution (정규 분포) : 연속 확률 분포의 일종으로, 중심극한정리를 따라 수집된 자료의 분포를 근사하는데 사용됨
Kalman Filter는 State Variable과 Noise가 모두 이 정규 분포를 따른다고 가정
- 서로 독립적인 데이터(Ex) 자연 현상)를 Sampling 할 경우 대부분 좌우대칭의 Gaussian Distribution을 따른다

- 각 변수는 평균(μ)과 표준편차(σ) 두 변수를 가짐
- 평균 (μ) : Random Distribution의 중심
- 표준편차 (σ) : Uncertainty. σ^2은 분산
- 위의 두 Parameter들에 의해 모양이 결정되고, 이 때의 분포를 N(μ,σ2)로 표시한다

- 중심극한정리 : 동일한 확률분포를 가진 독립 확률 변수 n개의 평균의 분포는 n이 적당히 크면 정규분포에 가까워진다는 정리

- 위 그래프는 확률밀도함수(Probability Density Function. PDF)로, 그래프의 면적을 통해 확률을 계산

- 위 그래프에서 이전 Step의 상태 변수 x^_k-1는 오른쪽 아래의 분포 N(μ, σ^2)를 갖는다
- 이 변수가 오른쪽 위의 선형 함수 y = ax + B를 통과한다
- 그래 인해 현재 Step에서의 상태변수 x^_k는 평균이 aμ + b이고 분산이 a^2 * σ^2를 갖는 Gaussian Distribution을 갖게 됨
- 위 과정이 Kalman Filter의 State Update 과정과 유사
4. Kalman Filter 동작 원리
How a Kalman filter works, in pictures | Bzarg
I have to tell you about the Kalman filter, because what it does is pretty damn amazing. Surprisingly few software engineers and scientists seem to know about it, and that makes me sad because it is such a general and powerful tool for combining informatio
www.bzarg.com
- 위 내용을 참고하여 정리한 Kalman Filter의 동작 과정
4.1 Example) 자율주행 Robot의 상태 추정
- 주행 중인 로봇의 상태를 아래와 같이 Position, Velocity로 가정
- 즉 Position, Velocity를 Robot의 State Variable로 사용

- 이 State Variable들의 값을 정확히 알긴 어려우나 아래처럼 가능한 범위는 예측이 가능하다

- 이 때 Kalman Filter는 p(position), v(velocity) 두 State Variable이 Gaussian Distribution을 따른다 가정
- 각 변수는 평균(μ)과 표준편차(σ) 두 변수를 가짐

- 가로축이 v, 새로축이 p의 Distribution
- 위 그림의 경우 v와 p의 distribution이 서로 상관관계를 갖지 않는 Uncorrelated 한 상태
- 한 변수의 상태를 통해 다른 변수의 상태를 알 수 없음
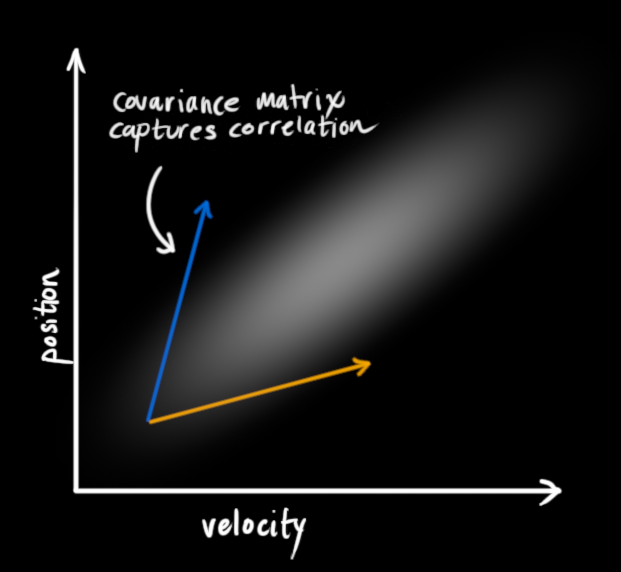
- 위 그림의 경우는 p와 v의 distribution이 서로 상관관계를 갖는 Correlated 한 상태
- 특정 velocity를 측정하면 특정 postiion을 알 수 있다
- 위와 같은 상관관계를 파악하면 더 많은 정보를 얻을 수 있음
- 한가지 측정값을 통해 다른 값을 예측할 수 있다
이러한 상관관계를 파악하는 것이 Kalman Filter의 목적: 알고싶은 변수를 다른 변수를 통해 간접적으로 추측혹은 불확실한 정보로부터 가능한 많은 정보를 얻는 것
- 위와 같은 상관관계는 Covariance Matrix(공분산)을 통해 얻을 수 있음
- 각 변수 Σij 는 i번째 상태 변수와 j번째 상태 변수의 상관관계를 나타냄
- Σij = Σji -> Symmetric Matrix(대칭 행렬)
Modeling by Gaussian Bolb
- Gaussian Distribution을 통해 State 추정값을 구하기 위해선 시간 t에서 아래의 두 정보가 필요
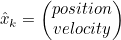

- x^_k : Best Estimation (앞의 평균 μ에 해당)
- Pk ; Covariance Matrix


- 이전 Time Step k-1에서의 State 추정값의 분포 통해 현재 Time Step k에서의 분포를 예측
- 특정 값을 예측하는 것이 아닌 분포를 예측
- Prediction Matrix Fk를 통해 이전의 State 추정값을 새 추정위치로 변환
- Fk를 통해 p, v를 예측하기 위해 아래의 기본적인 운동방정식을 Modeling에 사용
- 등속운동이라 가정하고 아래 공식 사용
이동 거리 = 이동 시간 x 속도

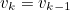
- 이후 pk, vk를 State Variable Matrix x^k로 묶고 각 State Variable들의 변화 계산을 Fk로 표현
- 즉 State Space Equation의 형태로 바꿈
- 이 Fk Matrix가 Kalman Filter 수식의 A Matrix
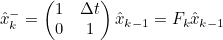
- 이를 통해 현재 Time Step에서의 State 예측값을 구함
- Covariance Matrix Pk는 아래의 과정을 통해 구함
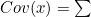
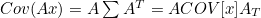
- 어떤 분포에 속하는 모든 점들을 A Matrix와 곱함
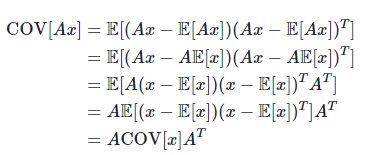
- 위의 두 식을 조합하면 아래와 같은 Modeling 결과가 나옴
- Kalman Filter의 추정, 오차 공분산 값 예측 과정 식 중 System Noise (Q)가 추가되지 않은 형태


- x^-k : 현재 Time Step에서의 State 예측
- Pk : 위 예측값의 Covariance 예측
External Influence 추가 (외부에서 System에 영향을 주는, 알고 있는 요인이 있을 경우 or Input에 의해 State가 변할 경우)
외부 영향이 없는 간단한 System일 경우 생략 가능
- 본 예제의 경우 Robot의 움직임을 나타내고, 이동 중에 가속도가 추가됨
- 이로 인해 속도가 변하므로 가속도 a를 External Influence로 추가
- a : Control Command에 의한 예측 가속
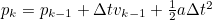

- 위를 다시 State Space Equation의 형태로 바꾸면
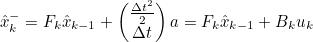
- Bk : Control Matrix
- uk : Control Vector
External Uncertainty 추가 (예상치 못한 외력에 의해 System이 Modeling 한 대로 움직이지 않는 경우) -> System Noise Qk 추가
- Ex) 드론 주행 중 바람에 의한 방해, 로봇 주행 중 미끄러짐 현상으로 인한 방해
- 이러한 외력이 System에 작용할 경우 이를 고려하지 않고 Modeling을 하였으므로 정확한 State 추정이 어려움
- 이 경우 매 Time Step마다 새로운 Uncertainty를 추가하여 Modeling에 표현 가능

- 기존 Distribution의 평균 xk-1을 Uncertainty가 추가된 Distribution으로 표현
- Gaussian Distribution을 통해 Uncertainty의 범위를 추측
- 위 그림의 경우 x^k는 xk-1이 평균인 분포에서 Qk의 Covariance를 갖는 분포로 이동
- 혹은 xk-1 가 Qk의 Covariance를 갖는 Noise가 있는 영역으로 이동 (외력을 Noise로 표현)

- 위 과정을 통해 이처럼 Noise가 추가된 Prediction 영역을 구할 수 있다
- 이를 수식에 표현하려면 기존의 수식에 공분산 Qk를 식에 추가해주면 됨
- 이는 Kalman Filter의 공분산 예측 과정에서의 System Noise Covariance Qk와 같다
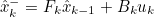
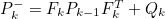
- 이로써 System 내/외부 모두에 Uncertainty가 존재
- uk : Known External Influence 만큼의 Correction (보정) 추가
- Qk : External Uncertainty 추가
Measurement 기반 Estimate Refine
- Sensor를 통해 System의 State를 간접적으로 추정
- position, velocity Sensor
예제에서는 Sensor를 통해 State를 직접 측정할 수 있다 가정하였으나, 보다 다양한 상황에서의 설명을 위해 Sensor로는 다른 값을 측정했다고 가정하고 풀이함

- 왼쪽 그래프는 지금까지의 과정을 통해 예측한 v - p 관계를 나타냄
- = 예측 State Variable
- 오른쪽 그래프는 그 예측 State Variable을 통해 예측한 Sensor 값
- = 예측 측정값
- 위 두 값 모두에 Noise가 있으므로 어느 하나를 정확한 값이라고 보기 어려움
- 이 때 예측 State 값을 예측 Sensor 값으로 변환해줘야 함
- Unit, Scale 차이를 맞춰줌

- Hk Matrix를 통해 예측 State 값을 예측 Sensor 값으로 변환
- 두 값의 unit, scale 차이를 맞춤

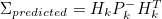

- 그리고 Sensor 측정값에도 Noise가 포함되어 있어 100% 신뢰할 순 없다
- 따라서 State 예측값을 특정 Sensor값으로 변환하지 않고 Sensor값의 범위로 변환

- Sensor 측정값은 Sensor Noise Rk 만큼의 Covariance를 갖는 Distribution 형태를 띰

- 실제로 Sensor로 측정되었어야 할 값 'real one'이 있으나 Noise로 인해 Sensor 값이 분포 형태로 나타날 수 있다

- 그 결과 총 2개의 Distribution이 나옴
- State 예측값을 예측 Sensor 측정값으로 변환한 값의 분포 (μexpected=Hkx^k 의 평균을 가짐)
- 실제 Sensor로 측정한 값의 분포 (의 평균을 갖는 분포)

- 위 두 Distribution 모두 타당성을 가지므로 둘의 교집합 부분을 사용


- 위의 교집합 부분이 각 Distribution에서의 추정값보다 더 정확함
- 두 Gaussian Distribution을 곱하여 교집합 부분의 평균과 공분산을 구함
Combining Gaussians
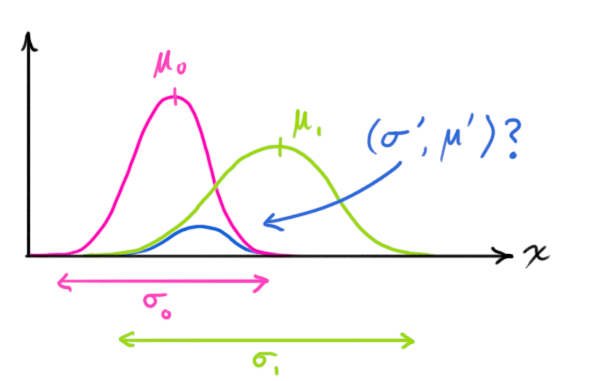
- 분홍색이 예측 Sensor 값, 연두색이 측정 Sensor 값에 대한 Distribution
- 파란색의 Unnormalized 된 곡선이 위 두 Gaussian Distribution의 교집합에 해당
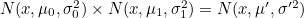
- 즉 두 Distribution을 곱하여 오른쪽 항의 새 Distribution을 구하는 것이 목표
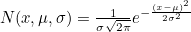
- 1차원 Gaussian Distribution Equation
- 이 식을 각 Distribution에 대입한 후 곱함
- 두 Gaussian PDF의 곱은 Gaussian PDF의 곱으로 정리됨


- 계산 결과
- 위 식 중 와


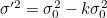
- 위가 1차원 Gaussian Distribution의 결합식
- 2차원의 경우는 아래처럼 σ^2 대신
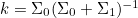

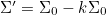
Kalman Filter Update 식 유도
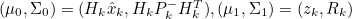
- 두 Distribution의 평균과 분산은 위와 같다
- 이 값들을 위의 Gaussian 결합의 평균과 분산 식에 대입

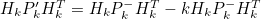
- 여기서 Kalman Gain은 아래와 같다

- 이에 Sensor 예측값의 Covariance 값을 대입하면
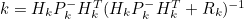
- 가 되고, 세 식의 계수들을 정리하면 아래와 같은 식이 나온다


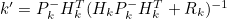
- 위 식은 Kalman Filter의 Update 과정 식에 해당한다
- Kalman Gain 계산, State 추정값 계산, 오차 Covariance 계산
- 위 식의 x^'k가 Kalman Filter의 출력에 해당하는 State 추정값
- Inverse Matrix가 있을 때만 이 계산 가능
- Inverse Matrix가 없다면 Pesudo - Inverse 적용 가능
4.2 Kalman Filter Information Flow

참고 자료 :
https://limitsinx.tistory.com/72
[제어시스템공학-4] Kalman Filter(칼만필터) 개념정리(1)
[Control Eng-1] Average Filter(평균필터) https://limitsinx.tistory.com/69 [Control Eng-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70 [Control Eng-3] Low Pass Filter(저주파 통과필터) https://limitsinx.tistory.com/7
limitsinx.tistory.com
https://gaussian37.github.io/autodrive-ose-table/
Optimal State Estimation 관련 글 목록
gaussian37's blog
gaussian37.github.io
칼만 필터는 어렵지 않아
칼만 필터는 어렵지 않아<br>http://www.hanbit.co.kr/store/books/look.php?p_code=B4956047798
fliphtml5.com
공분산 공식과 개념 / 분산과 차이 / 통계 분석
상관계수를 알아보려는 과정에서 공분산이라는 개념을 먼저 짚고 넘어가겠다 싶었다. 공분산이라고 하면 감...
blog.naver.com
가우시안(Gaussian) - 정규분포(Normal Distribution). 너란 분포 정말
정규분포 이야기. 확률과 통계를 한다면 정규분포에 대해서 귀에 딱지가 앉게 들었으니까, 가우시안분포(정규분포)를 들여다 보았으면 합니다. 우리가 정규분포를 언제 처음 만나냐면, "학생들
recipesds.tistory.com
https://wsstudynote.tistory.com/3
Kalman Filter
칼만 필터 (Kalman Filter) 칼만필터의 대략적인 개요는 아래와 같다 예측과 측정값을 통해 값을 추정하는 것이다. 기본이 되는 칼만 필터의 수식은 아래와 같다. - 시스템 모델 A, Q 를 기초로 하여 X^
wsstudynote.tistory.com
https://towardsdatascience.com/kalman-filter-interview-bdc39f3e6cf3
Kalman Filter Interview
I am currently into Term 2 of my Self Driving Car Nanodegree. Recently I met one of my colleagues Larry, who is a young developer and is…
towardsdatascience.com
'Study_Engineering' 카테고리의 다른 글
| Unscented Kalman Filter란 (0) | 2024.02.13 |
|---|---|
| Extended Kalman Filter란 (0) | 2024.01.16 |
| 표준편차, 분산, 공분산 (0) | 2024.01.16 |
| EKF를 통한 자율주행 로봇의 Localization (3) | 2024.01.15 |
| State Space Equation이란 (0) | 2024.01.12 |



