1. Extended Kalman Filter란
- Kalman Filter는 Linear System을 대상으로 함 (State Variable과 Noise가 Gaussian Distribution 형태를 갖는다 가정)
- 하지만 현실세계에선 대부분의 System이 Non-Linear System
- Non-Linear System에선 입력으로 Gaussian Distribution이 주어져도 결과는 Gaussian Distribution이 아니게 됨
- 따라서 평균 μ, 분산σ^2를 예측값의 정확도와 표준편차로 사용하지 못하므로 정확한 상태 추정 불가
- 이러한 Kalman Filter를 Non-Linear System에 적용할 수 있도록 Kalman Filter를 변형한 형태
- 이전 Timestep에서의 State 추정값을 통해 Linearization을 매 Timestep마다 진행한다
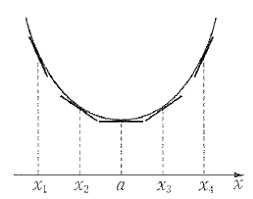
- 위처럼 Non Linear 함수 f(x), h(x)를 매순간마다 미분하여 Linearization 시킴
- Non Linear 함수의 매우 작은 부분을 짧은 직선으로 나눠 Prediction, Update Step의 선형화 계산에 사용
- 이 과정에서 1차 Taylor Series Expansion과 Jacobian이 활용됨
1.1 Taylor Series
- 임의의 함수를 무한개의 다항식을 더하여 근사하는 방식
- x가 a에 근사할 때 아래 다항식은 원 함수 f(x)에 근사함
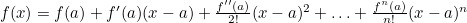
- 아래 그림과 같이 차수가 높아질수록 원 함수에 가까워짐
- 단 차수가 높아질수록 계산량이 많아지므로 주로 첫 번째 항만을 사용하여 근사화시킴
- EKF에서의 Linearization에도 1차 Taylor Series만을 사용
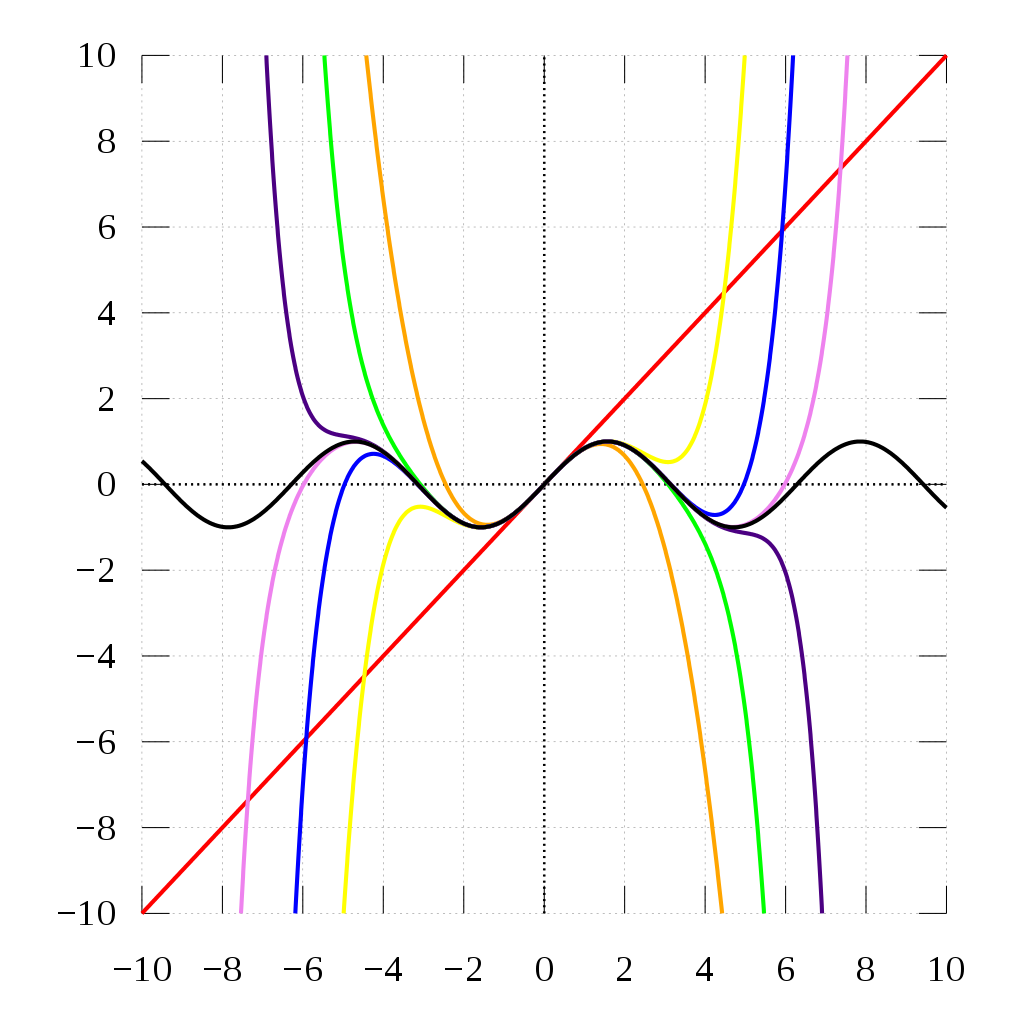
- 검은색 곡선이 Sine 함수, 빨강 (1차), 주황(3차), 노랑(5차), 초록(7차), 파랑(9차), 남색(11차), 보라(13차) 항까지 합한 곡선
- 항의 차수가 높아질수록 Sin 함수와 모양이 비슷해진다
1.2 Jacobian Matrix
- 함수의 요소들에 대해 모든 요소들을 1차 편미분한 Matrix
- 즉 다변수 Vector의 도함수 Matrix
- 미소 영역에서의 비선형 변환을 선형 변환으로 근사하여 다변수 다함수의 일차 미분을 나타내는데 사용함
- 매 순간 모든 Variable에 대해 편미분을 해 Linearization 된 값을 얻어냄
- System Modeling에 사용하는 State Space Equation에 따라 계산에 사용되는 Variable의 개수가 달라짐
- 이 모든 Variable에 대해 미분을 하기 위함
- 즉 입출력이 여러 개일 때, 각각의 입출력의 특성에 따라 Linearization을 진행하는 것

- 위와 같이 Non Linear 함수의 y1에서 dt 이후의 값 y2를 구하고자 할 때, Linearization Approximation을 통해 그 값을 구함

- 즉 이 Jacobian Matrix 계산을 통해 Non Linear 함수를 매순간 Linear 함수로 만들어 Kalman Filter를 적용시키는 것이 Extended Kalman Filter
- 위의 y1이 직전 Step에서의 추정치
- 함수 F가 아래와 같이 n개의 Variable을 가진 함수 m개의 집합일 때

- Jacobian Matrix는 아래와 같다

2. Linearization 과정


- 그림 (a)에서의 Linear System의 경우 이전 Timestep의 State Variable x^_k-1의 분포가 아래와 같을 때

- 오른쪽 위의 선형 함수 y = ax + B를 통과하면 현재 Timestep에서의 상태변수 x^_k는 아래와 같은 분포를 가짐
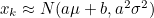
- 평균이 aμ + b이고 분산이 a^2 * σ^2를 갖는 Gaussian Distribution을 갖게 됨
- 위 과정이 Kalman Filter의 State Update 과정과 유사
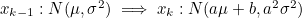
- 하지만 그림 (b)에서의 Non-Linear System의 경우 상태 과도(State Transistion)와 측정값이 비선형적이다
- 이로 인해 상태 과도를 Linear State Transisiton으로 나타낼 수 없다
- EKF는 상태 과도 확률(State Transistion Probability)와 측정 확률이 비선형 함수에 의해 조절된다 가정
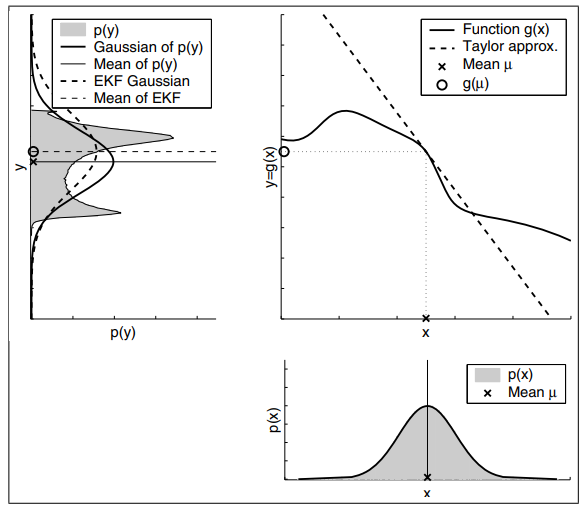
- State Variable x를 비선형 함수 g에 넣지 않고 g를 선형 근사화한 식에 입력으로 넣음
- 해당 선형 근사 함수는 함수 g의 평균 μ에서의 접선
- 위 선형 근사 과정에서 근사 오차가 발생하며, 그 정도는 왼쪽 위 그래프의 점선과 굵은 선 그래프의 차이만큼임
- 여기서 1차 Taylor Series를 통해 Linearizaiton을 진행하며 Non Linear Matrix f, h에 대한 자세한 Linearization 과정은 아래와 같다
2.1 System Model (f)

- System Model에 대한 1차 Taylor Series
- u는 입력, µ는 평균
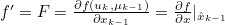
- 위의 F가 Jacobian Matrix
- f : System Model
- x : State Variable
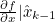
- 위는 행렬 ∂f/ ∂x에 x^_k를 대입하여 계산한 값이라는 뜻
- Jacobian Matrix도 uk, μk에 의존하므로 시간에 따라 값이 달라짐
2.2 Measurement Model (h)
- Measurement Model도 이와 동일한 과정을 통해 Linearization을 진행할 수 있다
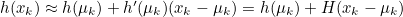
- Measurement Model에 대한 1차 Taylor Series

- 위의 H가 Jacobian Matrix
- h : xk에서의 측정값 zk에 대한 측정함수
즉 1차 Taylor Series를 통해 Non Linear System Model의 근사식을 나타내고
Jacobian Matrix 계산을 통해 System Model에 대한 Linearization 진행
- 이 Linearization 과정은 Extended Kalman Filter의 매 Step마다 이뤄짐
위처럼 직전 Step에서의 추정값을 실제 System의 State와 가장 근사한 값이라 가정하고 그 값을 기준으로 매 Step마다 새로운 Linear System Model 계산
(Extended Kalman Filter는 직전 Step의 State 추정값을 Linearization의 기준으로 삼음)
3. 전체 과정
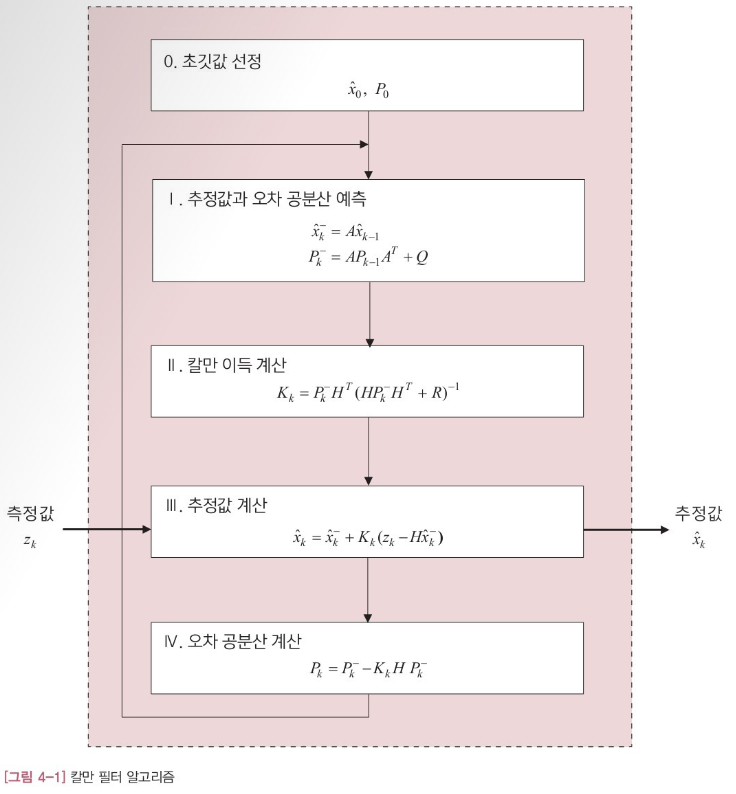

- 위의 Linearization 과정을 제외하곤 Kalman Filter와 동일한 과정을 거침
- 추정값 예측 식이 기존의 x^-_k = A*x_k-1에서 x^-_k = f(x^-_k-1)로 변형
- H matrix가 h로 변형
이 부분에서 Non-Linear 성분이 추가되며, Kalman Filter와의 유일한 차이점
(만약 두 Matrix 중 Linear Matrix가 있다면 Kalman Filter에서와 동일하게 계산)
- f : State Transisiton Model (Non Linear)
- 시간에 따른 상태의 변화를 나타내는 System Model

- A : 위 System Model의 Jacobian Matrix
- Kalman Filter에서의 A Matrix와 다름
- h : 측정값과 상태변수 사이의 관계를 나타내는 Measurement Model (Non Linear)
- H : 위 Measurement Model의 Jacobian Matrix
- 마찬가지로 Kalman Filter에서의 H Matrix와 다름
- A, H 두 Matrix가 Linearization 과정의 결과
- R : Measurement Noise의 Covariance Matrix
- Q : System Noise의 Covariance Matrix
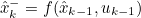
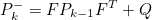
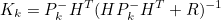

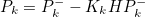
4. EKF의 한계점
- Non Linear 함수를 Linearization하여 State를 추정하므로, System의 비선형성이 클 시 State 추정값이 부정확해질 수 있다
5. EKF 활용 예제
EKF를 통한 자율주행 로봇의 Localization
목적 Extended Kalman Filter를 통해 주어진 환경에서 자율주행 Robot의 Localization (위치 파악) 진행 Wheel Encoder값으로부터 Odometry를 계산하고, IMU로부터 그 값에 Extended Kalman Filter를 적용시켜 로봇의 위치
youngseong.tistory.com
Estimating Battery`s SoC using EKF
0. 목표EKF를 통한 SOC Estimator 구현Matlab 상에서 Estimator Simulation을 통한 평가1. Equivalent Circuit Model아래와 같은 방전 전류 인가에 따른 Cell의 전압 반응을 Thevenin Equivalent Circuit으로 모사즉 Cell의 전기
youngseong.tistory.com
참고 자료 :
https://limitsinx.tistory.com/78
[제어시스템공학-10] Extended Kalman Filter(확장칼만필터) 개념
[제어시스템공학-1] Average Filter(평균필터) https://limitsinx.tistory.com/69 [제어시스템공학-2] Moving Average Filter(이동평균필터) https://limitsinx.tistory.com/70 [제어시스템공학-3] Low Pass Filter(저주파 통과필터) h
limitsinx.tistory.com
https://jml-note.tistory.com/entry/EKF-SLAM
EKF SLAM
Extended Kalman Filter 여러 종류의 칼만필터(Family members of Kalman Filter)(EKF) Jinyong 님 블로그 [SLAM] Kalman filter and EKF(Extended Kalman Filter) · Jinyong [SLAM] Kalman filter and EKF(Extended Kalman Filter) Kalman filter와 Extended
jml-note.tistory.com
https://soohwan-justin.tistory.com/47
Kalman Filters(3. Extended Kalman Filter and Unscented Kalman Filter)
이 포스트는 theconstructsim.com의 Kalman Filters 를 참고하였습니다. https://youtu.be/xwAPRhxdbfA 이번 포스트에서 다룰 내용은 비선형 함수를 다루기 위한 각각의 필터에 대한 이해 비선형 함수를 다루기 위
soohwan-justin.tistory.com
https://blog.naver.com/tlaja/220725335703
Gradient, Jacobian 행렬, Hessian 행렬, Laplacian
1.Gradient : 어떤 함수f 가 (x1,x2,x3,,,xn)변수로 구성되어 있다면 함수f 는 다변수 함수라고 하...
blog.naver.com
https://gaussian37.github.io/math-calculus-jacobian/
Jacobian(자코비안) 이란?
gaussian37's blog
gaussian37.github.io
https://ko.wikipedia.org/wiki/%ED%85%8C%EC%9D%BC%EB%9F%AC_%EA%B8%89%EC%88%98
테일러 급수 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 사인 함수의 테일러 급수의 수렴. 검은 선은 사인 함수의 그래프이며, 색이 있는 선들은 테일러 급수를 각각 1차(빨강), 3차(주황), 5차(노랑), 7차(초록), 9차(파랑
ko.wikipedia.org
https://minding-deep-learning.tistory.com/46
[칼만필터는 어렵지않아/Python] CH.12 확장 칼만 필터
Python 실습코드 참고 (tbmoon님의 Github) https://github.com/tbmoon/kalman_filter tbmoon/kalman_filter Kalman Filter in Python (파이썬으로 구현하는 칼만 필터). Contribute to tbmoon/kalman_filter development by creating an account on Git
minding-deep-learning.tistory.com
https://towardsdatascience.com/extended-kalman-filter-43e52b16757d
Extended Kalman Filter: Why do we need an Extended Version?
This post is in continuation to my last post on Kalman Filter. So my colleague Larry is pretty excited to know about the working of Kalman…
towardsdatascience.com
'Study_Engineering' 카테고리의 다른 글
| Nelder-Mead Algorithm 이란 (0) | 2024.05.03 |
|---|---|
| Unscented Kalman Filter란 (0) | 2024.02.13 |
| Kalman Filter란 (0) | 2024.01.16 |
| 표준편차, 분산, 공분산 (0) | 2024.01.16 |
| EKF를 통한 자율주행 로봇의 Localization (3) | 2024.01.15 |



