1. Nelder-Mead Algorithm이란
- 주어진 비선형 함수를 최소화하는 일반적인 Unconstrained Optimization 문제를 풀기 위해 설계된 Algorithm
- 즉, 아래처럼 n개의 점들을 갖는 비선형 함수를 하나의 직선으로 근사하기 위해 사용

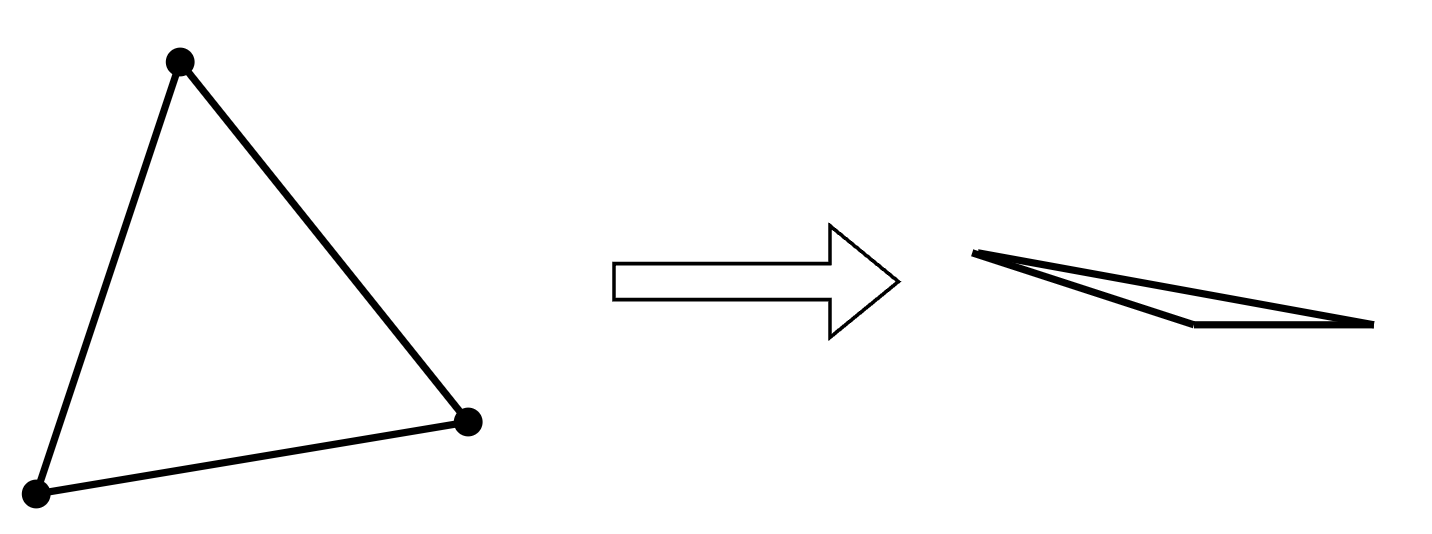
- 미분 불가능한 함수에서 최소 값을 찾는 방법으로, 다차원의 1) Unconstrained Optimization를 미분 없이 수행
- 미분 정보를 필요로 하지 않아 Non-Smooth한 함수에 적합
- 기본 이론이 단순하여 많은 분야에서 활용됨
- 함수의 값이 불확실하거나 Noise에 노출되는 경우의 Parameter 추정이나 비슷한 통계학적 문제들을 해결하는데 사용
- 또는 통계학이나 실험적 수학 계산에서 자주 발생하는 불연속적인 함수에 대한 문제를 해결하는데 사용
- 아래와 같은 특성으로 인해 Direct Search Method에 포함된다
- 일부 점 R^n에 대한 함수값만을 사용
- 또한 미분을 하지 않으므로 기울기와 관련된 계산이나 근사를 수행하지 않음
- 2) Simplex Method를 기반으로 Optimization을 진행
1.1. 관련 이론
1) Unconstrained Optimitzation
- 제약 조건이 없는 최적화 문제라는 뜻
- 변수의 값을 바꿔가며 목적 함수의 값을 최소/최대화 하는 변수 값을 찾는 것
2) Simplex Method (단체법)
- 두 개 이상의 변수를 가진 선형계획법의 최적해를 구하는 Algorithm
- 인접해 있는 극단점들의 목적함수의 값들을 계속 검토하여 최적해를 구하는 방법
- 임의의 가능해(초다면체의 정점)로부터 탐색을 시작
- 현재의 가능해와 인접하며 더욱 최적에 가까운 가능해로 옮겨가며 탐색을 진행
- 더 이상 옮겨갈 해가 없으면 최적해를 찾은 것
- 목적함수가 발산하거나 순환하면 해가 없을 수 있고, 동일한 목적값을 갖는 다수의 해가 존재할 수도 있다

- Ex) 두 변수 X1, X2의 제약 조건을 나타내는 식 5개가 있고, 목적함수 F가 있을 경우
- 목적함수 k값을 최대화하는 해 (X1, X2)는 아래 방정식들의 해 중 목적함수 F의 값을 최대화하는 값이다
1. 식 1)과 2)의 연립 방정식
2. 식 1)과 3)의 연립 방정식
... ...
... ...
... ...
9. 식 3)과 5)의 연립 방정식
10. 식 4)와 5)의 연립 방정식
- 함수 R^n 내의 Simplex S는 n+1(꼭짓점 x0, ... x_n+1)의 3) Convex Hull으로 정의된다
Ex) R^2의 Simplex는 삼각형이고, R^3의 Simplex는 사면체이다


3) Convex Hull
- 주어진 점 집합이나 영역을 포함하는 가장 작은 볼록 집합
- 2차원 좌표 평면 위에 존재하는 여러 점들 중 일부를 이용하여 모든 점을 포함하는 볼록 다각형
- Convex(볼록 함수) : 임의의 두 점을 이은 직선이 본래 곡선보다 위에 있는 함수. 수식으로 표현하면 아래와 같다

2. 동작 과정
0) Construct Simplex
- R^2인 함수에 대해 Nelder - Mead Algorithm을 적용
- 함수의 각 점들에 대한 Simplex를 구성
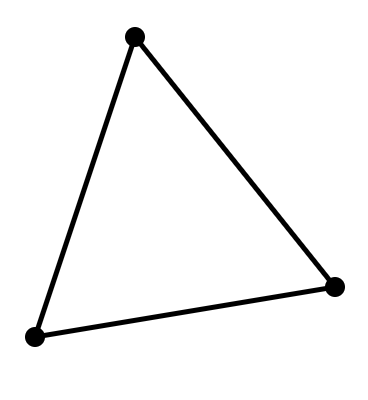
- 초기에 Simplex는 Nondegenerate 해야 한다
- 즉 각 점들이 서로 다른 초평면 위에 존재해야 한다
1) Ordering
- 각 함수 값들을 아래와 같이 크기 순으로 정렬 후 함수 값의 인자 h, s, l 값을 결정

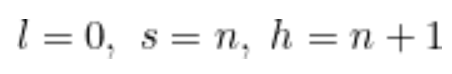
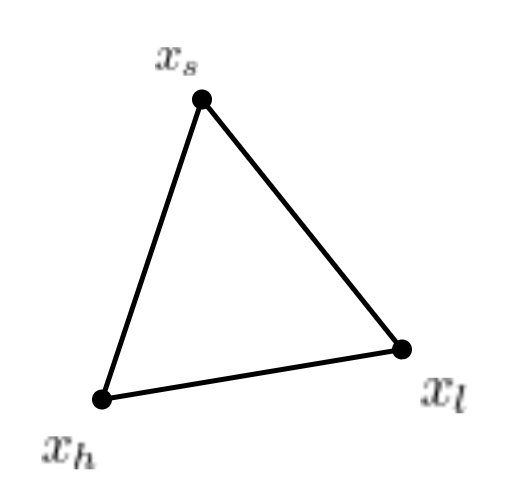
- 이후 Iteration을 계속 진행할지 멈출지 여부를 결정
- Simplex S가 어느 정도 충분히 작아지거나, 함수값들이 서로 충분히 가까워지면, 즉 함수가 연속이 되면 Iteration을 종료한다
- 현재 Simplex 함수값의 표준편차가 일정 수준 아래로 떨어지면 Iteration 종료 후 Simplex 내의 Xl 점이 최적의 값으로 반환됨
2) Centroid Point C 계산
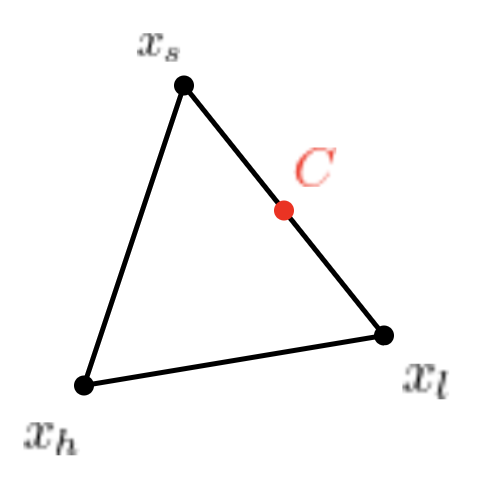
- 아래 수식을 통해 xh를 제외한 모든 점들 간의 Centriod점 C 계산

3) Reflection Point Xr 계산
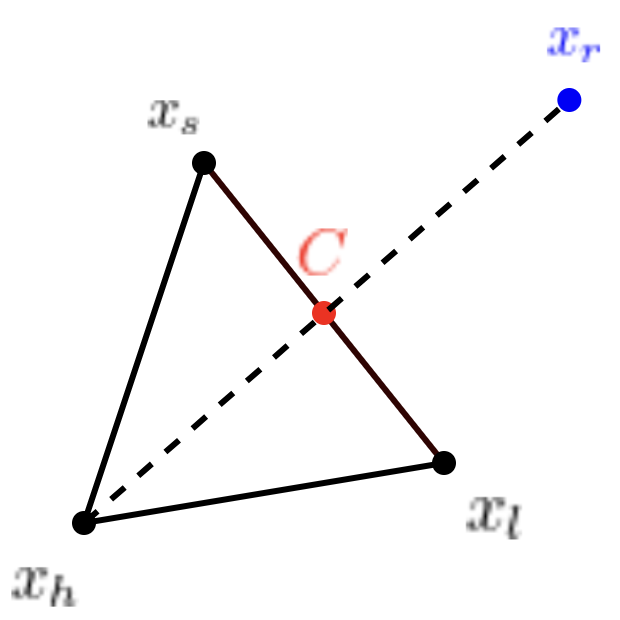
- 아래 수식을 통해 Xh와 C점이 형성한 선 상의 Rflection Point Xr 계산
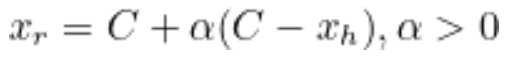
- 이후 Xr에서의 함수 값 계산
4) Simplex Transformation
- 아래 조건에 따라 Reflection / Expansion / Contraction 중 하나를 선택해 점 Xh 만을 더 나은 점으로 대체하는 Simplex Transformation 수행

- 위의 Simplex Transformation은 아래의 4개가지 Parameter들에 의해 조절된다
- α : Reflection
- β : Contraction
- γ : Expansion
- δ : Shrinkage
- 위 Parameter들은 아래 조건을 만족해야 하며, 표준 값은 그 아래와 같다


A. Reflection
- 점 Xh를 Xr로 대체한 후 1) Ordering 과정으로 이동

B. Expansion
- 아래 수식을 통해 Expansion Point Xe를 계산


- 만약 Xe점이 아래 조건을 만족하면, 점 Xh를 Xe로 대체 후 1) Ordering 과정으로 이동
- 만족하지 못할 경우 점 Xh를 Xr로 대체 후 1) Ordering 과정으로 이동

C. Contraction
가. Outside

- 위 조건에 해당할 경우, 아래 수식을 통해 Outside Contrction Point Xc 계산
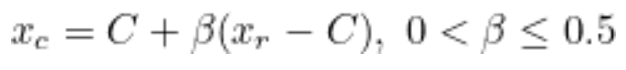
- 이후 점 Xc가 아래 조건을 만족할 경우 점 Xh를 Xc로 대체 후 1) Ordering 과정으로 이동

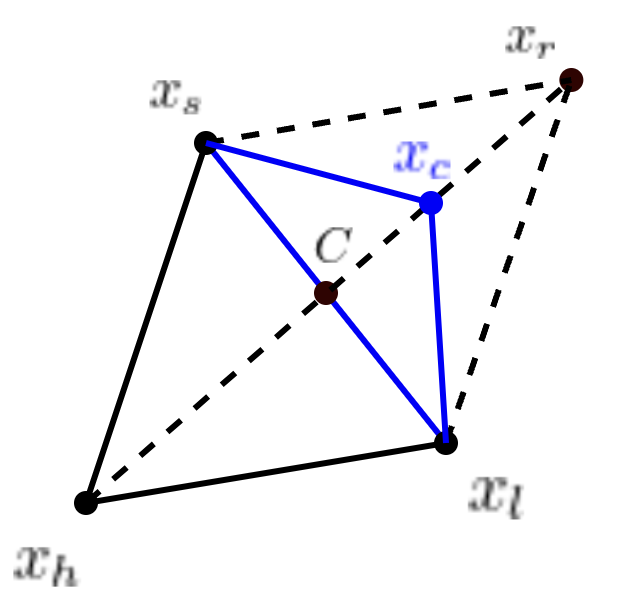
- 위 조건을 만족하지 못할 경우 5) Shrinkage 과정으로 이동
나. Inside

- 위 조건에 해당할 경우, 아래 수식을 통해 Inside Contraction Point Xc 계산
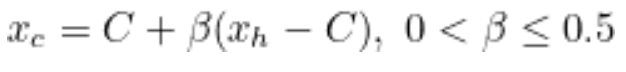
- 이후 점 Xc가 아래 조건을 만족할 경우 점 Xh를 Xc로 대체 후 1) Ordering 과정으로 이동


- 위 조건을 만족하지 못할 경우 5) Shrinkage 과정으로 이동
5) Shrinkage
- 아래 수식을 통해 Xl을 제외한 n개의 모든 Point들을 다시 계산
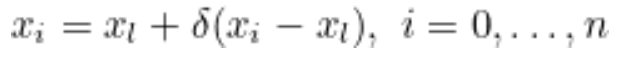

- 위의 Transformation 계산이 실패했을 경우 진입하는 과정
6) Transformation 과정 정리
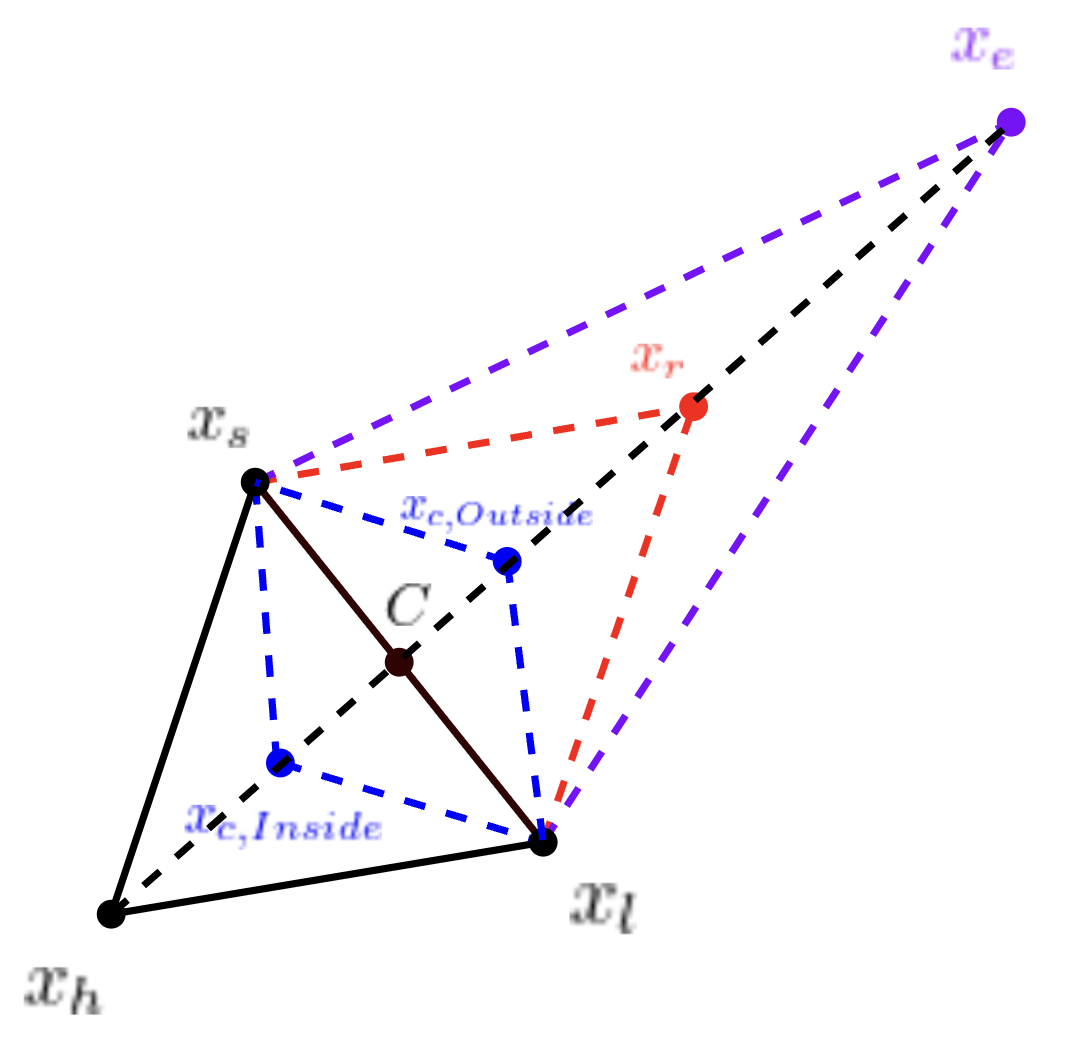
- 위의 Transformation 과정에서 모든 Test Point들은 xh와 C로 정의된 선 상에 존재하고, 최대 2개의 점들이 단일 반복으로 계산됨
- 위 과정이 성공하면, 받아들여진 점은 새 Simplex의 새 점이 됨
- 위 과정이 실패하면, xl점 쪽으로 Simplex가 수축함
- 이 경우, n개의 새로운 꼭짓점이 계산됨
- Simplex 상의 꼭짓점들 상에서 함수값이 감소하도록 하는 변환 과정을 수행
- 각 Step에서의 변환 과정은 하나 이상의 Test Point들을 해당 함수값과 함께 계산하고, 그 함수값을 꼭짓점의 값과 비교하여 결정된다
- 이러한 Nelder - Mead Algorithm은 각 Step에서 하나 혹은 두개만의 Function Evaluation이 요구된다
- 타 Direct Seacrch Method들의 경우 n개 혹은 그 이상의 Function Evaluation이 요구된다
참고 자료 : https://itgwangjin.github.io/posts/2019/04/Optimization%20-%20Nelder%20Mead%20simplex%20algorithm
Optimization - Nelder Mead simplex algorithm
Matlab function ‘fminsearch’ derive from Nelder Mead simplex algorithm.I has studied deep learning in the nick of time.So I will study this Nelder-Mead simplex algorithm while I am at it
itgwangjin.github.io
https://en.wikipedia.org/wiki/Nelder%E2%80%93Mead_method#Termination
Nelder–Mead method - Wikipedia
From Wikipedia, the free encyclopedia Numerical optimization algorithm Not to be confused with Dantzig's simplex algorithm for the problem of linear optimization. An iteration of the Nelder-Mead method over two-dimensional space. Search over the Rosenbrock
en.wikipedia.org
http://www.scholarpedia.org/article/Nelder-Mead_algorithm
Nelder-Mead algorithm - Scholarpedia
The Nelder-Mead algorithm or simplex search algorithm, originally published in 1965 (Nelder and Mead, 1965), is one of the best known algorithms for multidimensional unconstrained optimization without derivatives. This method should not be confused with Da
www.scholarpedia.org
[Optimization] Unconstrained (제약 조건이 없는 최적화 문제), Local minimum 판단, Critical points, FONC
Unconstrained Optimization : 제약 조건(constraints)이 없는 최적화 문제 제약 조건이 없는 최적화 문제란 변수의 값을 어떤 함수의 최솟값 또는 최댓값으로 만드는 것을 목적으로 하는 문제입니다. 변수
exvarx.tistory.com
https://ko.wikipedia.org/wiki/%EB%8B%A8%EC%B2%B4%EB%B2%95_(%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98)
단체법 (알고리즘) - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 이 문서에는 관련 분야의 전문가 참여가 필요합니다.이 분야를 잘 알고 계신다면 이 문서가 더 좋은 문서가 되도록 문서 수정을 도와주세요. 선형계획법에서
ko.wikipedia.org
https://terms.naver.com/entry.naver?docId=77068&cid=50315&categoryId=50315
심플렉스
두 개 이상의 변수를 가진 선형계획법(線型計劃法)의 해(解)를 구하는 방법으로, 인접해 있는 극단점(極端點)들의 목적함수의 값들을 계속 검토해서 최적해를 구하는 방법을 말한다.
terms.naver.com
https://david0506.tistory.com/62
컨벡스 헐(Convex Hull) 알고리즘
Convex Hull이란? Convex Hull은 2차원 좌표 평면 위에 존재하는 여러 점들 중 일부를 이용하여 모든 점을 포함하는 볼록 다각형이다. 아래와 같이 점들이 2차원 좌표 평면에 존재할 때, 볼록 껍질을 나
david0506.tistory.com
'Study_Engineering' 카테고리의 다른 글
| State Machine 이란 (0) | 2025.05.01 |
|---|---|
| Thread란 (0) | 2024.07.09 |
| Unscented Kalman Filter란 (0) | 2024.02.13 |
| Extended Kalman Filter란 (0) | 2024.01.16 |
| Kalman Filter란 (0) | 2024.01.16 |



